V této lekci se naučíme, jak stanovit spojitost funkce. Uděláme to pomocí limitek, tedy jednostranných - vpravo a vlevo, které nejsou vůbec děsivé, přestože se píšou jako a .
Ale co je vlastně kontinuita funkce? Dokud se nedostaneme k přísné definici, je nejjednodušší si představit čáru, kterou lze nakreslit bez zvednutí tužky z papíru. Pokud je taková čára nakreslena, pak je souvislá. Tato čára je grafem spojité funkce.
Graficky je funkce spojitá v bodě, pokud se její graf v tomto bodě „nerozbije“. Graf takové spojité funkce je ![]() zobrazeno na obrázku níže.
zobrazeno na obrázku níže.

Určení spojitosti funkce limitou. Funkce je spojitá v bodě, pokud jsou splněny tři podmínky:
1. Funkce je definována v bodě .
Pokud není splněna alespoň jedna z uvedených podmínek, není funkce v bodě spojitá. V tomto případě říkají, že funkce trpí nespojitostí a body na grafu, ve kterých je graf přerušen, se nazývají body nespojitosti funkce. Graf takové funkce, která trpí nespojitostí v bodě x=2, je na obrázku níže.

Příklad 1. Funkce F(X) je definován takto:
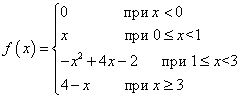
Bude tato funkce spojitá v každém z hraničních bodů svých větví, tedy v bodech X = 0 , X = 1 , X = 3 ?
Řešení. Zkontrolujeme všechny tři podmínky spojitosti funkce v každém hraničním bodě. První podmínka je splněna, od čeho funkce definována v každém z hraničních bodů vyplývá z definice funkce. Zbývá zkontrolovat zbývající dvě podmínky.
Tečka X= 0. V tomto bodě najdeme levý limit:
![]() .
.
Pojďme najít pravý limit:
X= 0 musí být nalezeno pro tu větev funkce, která obsahuje tento bod, tedy druhou větev. Najdeme je:
Jak vidíme, limita funkce a hodnota funkce v bodě X= 0 se rovnají. Funkce je tedy v bodě spojitá X = 0 .
Tečka X= 1. V tomto bodě najdeme levý limit:
Pojďme najít pravý limit:

Limita funkce a hodnota funkce v bodě X= 1 musí být nalezeno pro tu větev funkce, která obsahuje tento bod, tedy druhou větev. Najdeme je:
 .
.
Limita funkce a hodnota funkce v bodě X= 1 jsou stejné. Funkce je tedy v bodě spojitá X = 1 .
Tečka X= 3. V tomto bodě najdeme levý limit:
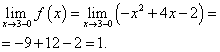
Pojďme najít pravý limit:

Limita funkce a hodnota funkce v bodě X= 3 musí být nalezeno pro tu větev funkce, která obsahuje tento bod, tedy druhou větev. Najdeme je:
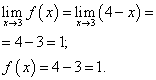 .
.
Limita funkce a hodnota funkce v bodě X= 3 se rovnají. Funkce je tedy v bodě spojitá X = 3 .
Hlavní závěr: tato funkce je spojitá v každém hraničním bodě.
Sami si stanovte kontinuitu funkce v určitém bodě a poté se podívejte na řešení
Spojitou změnu ve funkci lze definovat jako postupnou změnu bez skoků, ve které malá změna v argumentu znamená malou změnu funkce.
Ukažme si tuto plynulou změnu funkce na příkladu.

Na niti nad stolem nechte viset závaží. Vlivem tohoto zatížení se nit natahuje, takže vzdálenost l zatížení od bodu zavěšení závitu je funkcí hmotnosti břemene m, to je l = F(m) , m≥0 .
Pokud mírně změníte hmotnost nákladu, pak vzdálenost l se změní málo: malé změny m malé změny odpovídají l. Pokud se však hmotnost zátěže blíží pevnosti nitě v tahu, pak mírné zvýšení hmotnosti zátěže může způsobit přetržení nitě: vzdálenost l se náhle zvětší a bude se rovnat vzdálenosti od bodu zavěšení k povrchu stolu. Graf funkce l = F(m) znázorněno na obrázku. V řezu je tento graf souvislá (plná) čára a v bodě je přerušena. Výsledkem je graf skládající se ze dvou větví. Ve všech bodech kromě funkce l = F(m) je spojitý, ale v určitém bodě má diskontinuitu.
Studium spojitosti funkce může být buď samostatnou úlohou, nebo jednou z etap kompletního studia funkce a sestavení jejího grafu.
Spojitost funkce na intervalu
Nechte funkci y = F(X) definované v intervalu ] A, b[ a je spojitý v každém bodě tohoto intervalu. Pak se nazývá spojitý v intervalu ] A, b[ . Pojem spojitosti funkce na intervalech tvaru ]- ∞ je definován podobně, b[ , ]A, + ∞[ , ]- ∞, + ∞[ . Nyní funkci y = F(X) definovaný na intervalu [ A, b]. Rozdíl mezi intervalem a segmentem: hraniční body intervalu nejsou zahrnuty v intervalu, ale hraniční body segmentu jsou zahrnuty v segmentu. Zde bychom měli zmínit tzv. jednostrannou kontinuitu: v bodě A, zůstávající v segmentu [ A, b] , můžeme se přiblížit pouze zprava a k bodu b- pouze vlevo. Říká se, že funkce je spojitá na intervalu [ A, b] , pokud je spojitý ve všech vnitřních bodech tohoto segmentu, spojitý vpravo v bodě A a je v bodě ponechána spojitá b.
Příkladem spojité funkce může být kterákoli z elementárních funkcí. Každá elementární funkce je spojitá na libovolném intervalu, na kterém je definována. Například funkce a jsou spojité v libovolném intervalu [ A, b], funkce je spojitá na intervalu [ 0 , b] , funkce je spojitá na jakémkoli segmentu, který neobsahuje bod A = 2 .
Příklad 4. Prozkoumejte spojitost funkce.
Řešení. Zkontrolujeme první podmínku. Funkce není definována v bodech - 3 a 3. Není splněna alespoň jedna z podmínek návaznosti funkce podél celé číselné osy. Proto je tato funkce v intervalech spojitá
.Příklad 5. Určete, při jaké hodnotě parametru A nepřetržitě po celou dobu doména definice funkce 
Řešení.
Najdeme pravý limit na:
![]() .
.
Je zřejmé, že hodnota v bodě X= 2 by se mělo rovnat sekera :
![]()
A = 1,5 .
Příklad 6. Určete, při jakých hodnotách parametrů A A b nepřetržitě po celou dobu doména definice funkce 
Řešení.
Pojďme najít levostrannou limitu funkce v bodě:
![]() .
.
Hodnota v bodě tedy musí být 1:
Najdeme funkci levé ruky v bodě:
Je zřejmé, že hodnota funkce v bodě by se měla rovnat:
Odpověď: funkce je spojitá v celém definičním oboru kdy A = 1; b = -3 .
Základní vlastnosti spojitých funkcí
Ke konceptu spojité funkce se matematika dostala především studiem různých pohybových zákonů. Prostor a čas jsou nekonečné a závislost například cesty s od času t, vyjádřené zákonem s = F(t) , uvádí příklad spojitého funkcí F(t). Teplota ohřáté vody se také plynule mění, je to také spojitá funkce času: T = F(t) .
V matematické analýze jsou prokázány některé vlastnosti, které spojité funkce mají. Pojďme si představit nejdůležitější z těchto vlastností.
1. Pokud funkce spojitá na intervalu nabývá hodnot různých znamének na koncích intervalu, pak v určitém bodě tohoto intervalu nabývá hodnoty rovné nule. Ve více formálním prohlášení, tato vlastnost je dána ve větě známé jako první Bolzano-Cauchy teorém.
2. Funkce F(X), spojité na intervalu [ A, b] , přebírá všechny střední hodnoty mezi hodnotami v koncových bodech, tedy mezi F(A) A F(b). Ve formálnějším vyjádření je tato vlastnost dána větou známou jako druhá Bolzanova-Cauchyho věta.
Určení spojitosti funkce v bodě
Funkce f (X) volal spojitý v bodě x 0
sousedství U (x0) tento bod, a pokud limita jako x inklinuje k x 0
existuje a je rovna hodnotě funkce v x 0
:
.
To znamená, že x 0 - to je konečný bod. Funkční hodnota v něm může být pouze konečné číslo.
Definice kontinuity vpravo (vlevo)
Funkce f (X) volal spojitá vpravo (vlevo) v bodě x 0
, je-li definována na nějakém pravostranném (levostranném) okolí tohoto bodu a je-li pravá (levá) mez v bodě x 0
rovna funkční hodnotě v x 0
:
.
Příklady
Příklad 1
Pomocí definic Heine a Cauchy dokažte, že funkce je spojitá pro všechna x.
Nechť existuje libovolné číslo. Dokažme, že daná funkce je v bodě spojitá. Funkce je definována pro všechna x . Proto je definován v bodě a v kterémkoli z jeho sousedství.
Používáme Heineho definici
Použijme . Nechť existuje libovolná posloupnost konvergující k : . Aplikováním vlastnosti limity součinu posloupností máme:
.
Protože existuje libovolná posloupnost konvergující k , pak
.
Kontinuita byla prokázána.
Používáme Cauchyho definici
Použijme .
Podívejme se na případ. Máme právo uvažovat funkci v jakémkoli okolí bodu. Proto to budeme předpokládat
(A1.1) .
Aplikujme vzorec:
.
S ohledem na (A1.1) provádíme následující odhad:
;
(A1.2) .
Při použití (A1.2) odhadneme absolutní hodnotu rozdílu:
;
(A1.3) .
.
Podle vlastností nerovnic, jestliže (A1.3) je splněno, jestliže a jestliže , pak .
.
Nyní se podívejme na pointu. V tomto případě
.
.
.
To znamená, že funkce je v bodě spojitá.
Podobným způsobem lze dokázat, že funkce , kde n je přirozené číslo, je spojitá na celé reálné ose.
Příklad 2
Pomocí dokažte, že funkce je spojitá pro všechny.
Daná funkce je definována na . Dokažme, že je v bodě spojitý.
Podívejme se na případ.
Máme právo uvažovat funkci v jakémkoli okolí bodu. Proto to budeme předpokládat
(A2.1) .
Aplikujme vzorec:
(A2.2) .
Dejme tomu. Pak
.
S ohledem na (A2.1) provádíme následující odhad:
.
Tak,
.
Aplikováním této nerovnosti a pomocí (A2.2) odhadneme rozdíl:
.
Tak,
(A2.3) .
Zavedeme kladná čísla a spojíme je s následujícími vztahy:
.
Podle vlastností nerovnic, jestliže (A2.3) je splněno, jestliže a jestliže , pak .
To znamená, že pro každé pozitivum vždy existuje . Pak pro všechna x vyhovující nerovnosti je automaticky splněna následující nerovnost:
.
To znamená, že funkce je v bodě spojitá.
Nyní se podívejme na pointu. Musíme ukázat, že daná funkce je v tomto bodě vpravo spojitá. V tomto případě
.
Zadejte kladná čísla a:
.
To ukazuje, že pro každé pozitivní je vždy . Pak pro všechna x taková, že platí následující nerovnost:
.
Znamená to, že . To znamená, že funkce je spojitá vpravo v bodě.
Podobným způsobem lze dokázat, že funkce , kde n je přirozené číslo, je spojitá pro .
Reference:
O.I. Bešov. Přednášky o matematické analýze. Část 1. Moskva, 2004.
L.D. Kudrjavcev. Kurz matematické analýzy. Svazek 1. Moskva, 2003.
CM. Nikolského. Kurz matematické analýzy. Svazek 1. Moskva, 1983.
Nechte bod A patří do oblasti specifikace funkcí f(x) a jakékoli ε - sousedství bodu A obsahuje odlišné od A body oblasti specifikace funkce f(x), tj. tečka A je limitním bodem množiny (X), na kterém je funkce specifikována f(x).
Definice. Funkce f(x) nazývá se spojitý v bodě A, pokud funkce f(x) má na místě A limit a tento limit je roven konkrétní hodnotě f(a) funkcí f(x) na místě A.
Z této definice máme následující podmínka kontinuity funkce f(x) na místě A :
Od , pak můžeme psát
![]()
Tedy pro souvislou čáru v bodě A funkce symbol přechodu limitu a symbol F funkční charakteristiky lze zaměnit.
Definice. Funkce f(x) se nazývá spojitý vpravo (vlevo) v bodě A, je-li pravá (levá) mez této funkce v bodě A existuje a rovná se soukromé hodnotě f(a) funkcí f(x) na místě A.
Skutečnost, že funkce f(x) spojitý v bodě A napravo to napište takto:
A kontinuita funkce f(x) na místě A vlevo je napsáno jako:
Komentář. Body, ve kterých funkce nemá vlastnost spojitosti, se nazývají body nespojitosti této funkce.
Teorém. Nechť jsou funkce dány na stejné množině f(x) A g(x), spojitý v bodě A. Pak funkce f(x)+g(x), f(x)-g(x), f(x) g(x) A f(x)/g(x)- spojitý v bodě A(v případě soukromého je nutné dodatečně vyžadovat g(a) ≠ 0).
Spojitost základních elementárních funkcí
1) Funkce napájení y=x n s přírodním n souvisle na celé číselné řadě.
Nejprve se podívejme na funkci f(x)=x. Podle první definice limity funkce v bodě A vzít libovolnou sekvenci (xn), konvergující k A, pak odpovídající posloupnost funkčních hodnot (f(x n) = x n) bude také konvergovat A, to je ![]() , tedy funkce f(x)=x spojitý v libovolném bodě číselné osy.
, tedy funkce f(x)=x spojitý v libovolném bodě číselné osy.
Nyní zvažte funkci f(x)=x n, Kde n je tedy přirozené číslo f(x)=x · x · … · x. Pojďme k limitu na x → a, dostaneme , tedy funkci f(x)=x n průběžné na číselné ose.
2) Exponenciální funkce.
Exponenciální funkce y=a x na a>1 je spojitá funkce v libovolném bodě na nekonečné přímce.
Exponenciální funkce y=a x na a>1 splňuje podmínky:
3) Logaritmická funkce.
Logaritmická funkce je spojitá a rostoucí podél celé polopřímky x>0 na a>1 a je spojitý a klesá podél celé polopřímky x>0 na 0
4) Hyperbolické funkce.
Následující funkce se nazývají hyperbolické funkce:
Z definice hyperbolických funkcí vyplývá, že hyperbolický kosinus, hyperbolický sinus a hyperbolický tangens jsou definovány na celé číselné ose a hyperbolický kotangens je definován všude na číselné ose, s výjimkou bodu. x=0.
Hyperbolické funkce jsou spojité v každém bodě svého oboru (vyplývá to ze spojitosti exponenciální funkce a věty o aritmetických operacích).
5) Funkce napájení
Funkce napájení y=x α =a α log a x spojitý v každém bodě otevřené polopřímky x>0.
6) Goniometrické funkce.
Funkce hřích x A cos x kontinuální v každém bodě X nekonečná přímka. Funkce y=tan x (kπ-π/2,kπ+π/2) a funkce y=ctg x průběžně v každém intervalu ((k-1)π,kπ)(tady všude k- libovolné celé číslo, tzn. k=0, ±1, ±2, …).
7) Inverzní goniometrické funkce.
Funkce y=arcsin x A y=arccos x kontinuální na segmentu [-1, 1] . Funkce y=arctg x A y=arcctg x spojitý na nekonečné linii.
Dvě úžasné limity
Teorém. Funkční limit (hřích x)/x na místě x=0 existuje a je roven jedné, tzn.
![]()
Tato hranice se nazývá první pozoruhodný limit.
Důkaz. Na 0
![]()
![]()
Tyto nerovnosti platí i pro hodnoty X, splňující podmínky -π/2 ![]() . Protože cos x je tedy spojitá funkce
. Protože cos x je tedy spojitá funkce ![]() . Tedy pro funkce cos x, 1 a v některých δ
- sousedství bodu x=0 jsou splněny všechny podmínky teorémů. Proto,
. Tedy pro funkce cos x, 1 a v některých δ
- sousedství bodu x=0 jsou splněny všechny podmínky teorémů. Proto, ![]() .
.
Teorém. Funkční limit ![]() na x → ∞ existuje a rovná se číslu E:
na x → ∞ existuje a rovná se číslu E:
![]()
Tato hranice se nazývá druhá pozoruhodná hranice.
Komentář. To je také pravda
![]()
Spojitost komplexní funkce
Teorém. Nechte funkci x=φ(t) spojitý v bodě A a funkce y=f(x) spojitý v bodě b=φ(a). Pak komplexní funkce y=f[φ(t)]=F(t) spojitý v bodě A.
Nechat x=φ(t) A y=f(x)- nejjednodušší elementární funkce s mnoha hodnotami (X) funkcí x=φ(t) je rozsah funkce y=f(x). Jak víme, elementární funkce jsou spojité v každém bodě daného oboru. Proto podle předchozí věty komplexní funkce y=f(φ(t)), tedy superpozice dvou elementárních funkcí, je spojitá. Například funkce je spojitá v libovolném bodě x ≠ 0, jako komplexní funkce dvou elementárních funkcí x=t-1 A y = hřích x. Také funkce y=ln sin x spojitý v libovolném bodě intervalu (2kπ,(2k+1)π), k ∈ Z (hřích x>0).
Studium funkce pro spojitost v bodě se provádí podle již zavedeného rutinního schématu, které se skládá z kontroly tří podmínek spojitosti:
Příklad 1
Prozkoumejte spojitost funkce. Určete povahu nespojitostí funkcí, pokud existují. Proveďte výkres.
Řešení:
1) Jediným bodem v rozsahu je, kde funkce není definována.

Jednostranné limity jsou konečné a rovné.
V bodě tedy funkce trpí odstranitelnou diskontinuitou.
Jak vypadá graf této funkce?
Rád bych to zjednodušil ![]() a zdá se, že se získá obyčejná parabola. ALE původní funkce není definována v bodě , takže je vyžadována následující klauzule:
a zdá se, že se získá obyčejná parabola. ALE původní funkce není definována v bodě , takže je vyžadována následující klauzule:
Udělejme nákres: 
Odpovědět: funkce je spojitá na celé číselné ose kromě bodu, ve kterém trpí odstranitelnou diskontinuitou.
Funkce může být dále definována dobře nebo ne tak dobře, ale podle podmínky to není vyžadováno.
Říkáte, že je to přitažený příklad? Vůbec ne. To se v praxi stalo desítkykrát. Téměř všechny úkoly webu pocházejí ze skutečné nezávislé práce a testů.
Pojďme se zbavit našich oblíbených modulů:
Příklad 2
Funkce Prozkoumat ![]() pro kontinuitu. Určete povahu nespojitostí funkcí, pokud existují. Proveďte výkres.
pro kontinuitu. Určete povahu nespojitostí funkcí, pokud existují. Proveďte výkres.
Řešení: Z nějakého důvodu se studenti bojí a nemají rádi funkce s modulem, ačkoli na nich není nic složitého. Takových věcí jsme se už v lekci trochu dotkli. Geometrické transformace grafy
. Protože modul není záporný, je rozšířen takto: ![]() , kde „alfa“ je nějaký výraz. V tomto případě a naše funkce by měla být zapsána po částech:
, kde „alfa“ je nějaký výraz. V tomto případě a naše funkce by měla být zapsána po částech: 
Ale zlomky obou kusů musí být sníženy o . Snížení se stejně jako v předchozím příkladu neobejde bez následků. Původní funkce není v bodě definována, protože jmenovatel je nulový. Proto by měl systém dodatečně specifikovat podmínku a zpřísnit první nerovnost: 
Nyní o VELMI UŽITEČNÉ technice rozhodování: před finalizací úkolu na návrhu je výhodné zhotovit výkres (bez ohledu na to, zda to vyžadují podmínky či nikoliv). To za prvé pomůže okamžitě vidět body spojitosti a body nespojitosti a za druhé vás to 100% ochrání před chybami při hledání jednostranných limitů.
Pojďme udělat kresbu. V souladu s našimi výpočty je nalevo od bodu nutné nakreslit fragment paraboly(modrá barva) a vpravo je kousek paraboly (červená barva), přičemž funkce není definována v samotném bodě: 
Pokud máte pochybnosti, vezměte několik hodnot x a zapojte je do funkce ![]() (pamatujte na to, že modul zničí možné znaménko mínus) a zkontrolujte graf.
(pamatujte na to, že modul zničí možné znaménko mínus) a zkontrolujte graf.
Prozkoumejme funkci pro spojitost analyticky:
1) Funkce není v bodě definována, takže můžeme rovnou říci, že v něm není spojitá.
2) Stanovme povahu diskontinuity, abychom to udělali, vypočítáme jednostranné limity: 
Jednostranné limity jsou konečné a různé, což znamená, že funkce trpí nespojitostí 1. druhu se skokem v bodě . Všimněte si, že nezáleží na tom, zda je funkce v bodě přerušení definována nebo ne.
Teď už jen zbývá přenést kresbu z předlohy (byl vyroben jakoby s pomocí výzkumu ;-)) a splnit úkol:
Odpovědět: funkce je spojitá na celé číselné ose kromě bodu, ve kterém trpí nespojitostí prvního druhu se skokem.
Někdy vyžadují další indikaci skoku diskontinuity. Počítá se jednoduše - od pravé limity je potřeba odečíst levou limitu: , tedy v bodě zlomu naše funkce poskočila o 2 jednotky dolů (jak nám říká znaménko mínus).
Příklad 3
Funkce Prozkoumat ![]() pro kontinuitu. Určete povahu nespojitostí funkcí, pokud existují. Udělejte nákres.
pro kontinuitu. Určete povahu nespojitostí funkcí, pokud existují. Udělejte nákres.
Toto je příklad, který můžete vyřešit sami, vzorové řešení na konci lekce.
Přejděme k nejoblíbenější a nejrozšířenější verzi úlohy, kdy se funkce skládá ze tří částí:
Příklad 4
Prozkoumejte spojitost funkce a nakreslete graf funkce
 .
.
Řešení: je zřejmé, že všechny tři části funkce jsou spojité na odpovídajících intervalech, takže zbývá zkontrolovat pouze dva body „spojení“ mezi kusy. Nejprve si udělejme návrh výkresu. Techniku stavby jsem dostatečně podrobně komentoval v první části článku. Jediná věc je, že musíme pečlivě sledovat naše singulární body: kvůli nerovnosti hodnota patří přímce (zelená tečka) a kvůli nerovnosti hodnota patří parabole (červená tečka): 
No, v zásadě je vše jasné =) Zbývá pouze formalizovat rozhodnutí. Pro každý ze dvou „spojovacích“ bodů standardně kontrolujeme 3 podmínky spojitosti:
já)
1) ![]()

Jednostranné limity jsou konečné a různé, což znamená, že funkce trpí nespojitostí 1. druhu se skokem v bodě .
Vypočítejme skok diskontinuity jako rozdíl mezi pravým a levým limitem:
, to znamená, že se graf trhl o jednu jednotku nahoru.
II) Zkoumáme bod pro spojitost
1) ![]() - funkce je definována v daném bodě.
- funkce je definována v daném bodě.
2) Najděte jednostranné limity:

![]() - jednostranné limity jsou konečné a rovné, což znamená, že existuje obecná limita.
- jednostranné limity jsou konečné a rovné, což znamená, že existuje obecná limita.
3) ![]()
V konečné fázi převedeme kresbu do konečné verze, po které vložíme konečný akord:
Odpovědět: funkce je spojitá na celé číselné ose, kromě bodu, ve kterém trpí nespojitostí prvního druhu se skokem.
Příklad 5
Prozkoumejte spojitost funkce a sestrojte její graf  .
.
Jedná se o příklad samostatného řešení, krátké řešení a přibližnou ukázku úlohy na konci lekce.
Můžete nabýt dojmu, že v jednom bodě musí být funkce spojitá a v jiném musí být diskontinuita. V praxi tomu tak vždy není. Pokuste se nezanedbat zbývající příklady - bude zde několik zajímavých a důležitých funkcí:
Příklad 6
Daná funkce  . Prozkoumejte funkci pro spojitost v bodech. Sestavte graf.
. Prozkoumejte funkci pro spojitost v bodech. Sestavte graf.
Řešení: a znovu okamžitě proveďte kresbu na konceptu: 
Zvláštností tohoto grafu je, že po částech je funkce dána rovnicí osy úsečky. Zde je tato oblast nakreslena zeleně, ale v poznámkovém bloku je obvykle zvýrazněna tučně jednoduchou tužkou. A samozřejmě nezapomeňte na naše berany: hodnota patří do větve tečny (červená tečka) a hodnota patří do přímky.
Z výkresu je vše jasné - funkce je souvislá podél celé číselné osy, zbývá pouze formalizovat řešení, které je dovedeno do plné automatizace doslova po 3-4 podobných příkladech:
já) Zkoumáme bod pro spojitost
2) Vypočítejme jednostranné limity:

![]() , což znamená, že existuje obecný limit.
, což znamená, že existuje obecný limit.
Stala se tu malá legrační věc. Faktem je, že jsem vytvořil spoustu materiálů o limitech funkce, a několikrát jsem chtěl, ale několikrát jsem zapomněl na jednu jednoduchou otázku. A tak jsem se neuvěřitelnou snahou vůle přinutil neztratit myšlenku =) S největší pravděpodobností někteří čtenáři „atrapy“ pochybují: jaká je hranice konstanty? Limita konstanty je rovna konstantě samotné. V tomto případě je limit nuly rovna nule samotné (levotočivý limit).
3) ![]() - limita funkce v bodě je rovna hodnotě této funkce v daném bodě.
- limita funkce v bodě je rovna hodnotě této funkce v daném bodě.
Funkce je tedy spojitá v bodě podle definice spojitosti funkce v bodě.
II) Zkoumáme bod pro spojitost
1) - funkce je definována v daném bodě.
2) Najděte jednostranné limity:

A zde, v pravé hranici, je hranice jednoty rovna jednotě samotné.
![]() - existuje obecný limit.
- existuje obecný limit.
3)  - limita funkce v bodě je rovna hodnotě této funkce v daném bodě.
- limita funkce v bodě je rovna hodnotě této funkce v daném bodě.
Funkce je tedy spojitá v bodě podle definice spojitosti funkce v bodě.
Jako obvykle po průzkumu převedeme náš výkres do konečné verze.
Odpovědět: funkce je v bodech spojitá.
Vezměte prosím na vědomí, že ve stavu, kdy jsme nebyli dotázáni na nic o studiu celé funkce pro spojitost, a je považováno za dobrou matematickou formu formulovat přesné a jasné odpověď na položenou otázku. Mimochodem, pokud podmínky nevyžadují, abyste sestavili graf, pak máte plné právo jej nesestavit (ačkoli vás k tomu může později učitel donutit).
Malý matematický „překrucovač jazyka“, který si můžete sami vyřešit:
Příklad 7
Daná funkce  .
.
Prozkoumejte funkci pro spojitost v bodech. Klasifikujte body přerušení, pokud existují. Proveďte výkres.
Pokuste se správně „vyslovit“ všechna „slova“ =) A nakreslete graf přesněji, přesnost, nebude to všude zbytečné;-)
Jak si vzpomínáte, doporučoval jsem okamžitě dokončit výkres jako koncept, ale čas od času narazíte na příklady, kdy nemůžete okamžitě zjistit, jak graf vypadá. Proto je v řadě případů výhodné nejprve najít jednostranné limity a až poté na základě studie větve znázornit. V posledních dvou příkladech se také naučíme techniku pro výpočet některých jednostranných limit:
Příklad 8
Prozkoumejte spojitost funkce a sestrojte její schematický graf.
Řešení: špatné body jsou zřejmé: (sníží jmenovatel exponentu na nulu) a (sníží jmenovatel celého zlomku na nulu). Není jasné, jak vypadá graf této funkce, což znamená, že je lepší nejprve provést průzkum:
já) Zkoumáme bod pro spojitost
2) Najděte jednostranné limity:
Dávejte pozor na typická metoda pro výpočet jednostranné limity: místo „x“ dosadíme . Ve jmenovateli není žádný zločin: „sčítání“ „minus nula“ nehraje roli a výsledek je „čtyři“. Ale v čitateli se odehrává malý thriller: nejprve zabijeme -1 a 1 ve jmenovateli ukazatele, což má za následek . Jednotka děleno , se rovná „minus nekonečnu“, proto: . A nakonec „dva“ dovnitř nekonečně velký záporný stupeň rovna nule: . Nebo abych byl ještě konkrétnější: ![]() .
.
Vypočítejme pravou hranici:
A zde - místo „X“ dosadíme . Ve jmenovateli opět nehraje roli „aditivum“: . V čitateli se provádějí akce podobné předchozímu limitu: zničíme protilehlá čísla a vydělíme jedno : ![]()
Pravá limita je nekonečná, což znamená, že funkce trpí nespojitostí 2. druhu v bodě .
II) Zkoumáme bod pro spojitost
1) Funkce v tomto bodě není definována.
2) Vypočítejme levostrannou mez:
Metoda je stejná: do funkce dosadíme „X“. V čitateli není nic zajímavého - vyjde to jako konečné kladné číslo. A ve jmenovateli otevřeme závorky, odstraníme „trojky“ a „přísada“ hraje rozhodující roli.
Výsledkem je, že konečné kladné číslo děleno nekonečně malé kladné číslo, dává „plus nekonečno“: .
Pravá hranice je jako dvojče, s jedinou výjimkou, že se objevuje ve jmenovateli nekonečně malé záporné číslo:
Jednostranné limity jsou nekonečné, což znamená, že funkce trpí nespojitostí 2. druhu v bodě .
Máme tedy dva body zlomu a samozřejmě tři větve grafu. Pro každou větev je vhodné provést stavbu bod po bodu, tzn. vezměte několik hodnot „x“ a dosaďte je do . Upozorňujeme, že podmínka umožňuje sestavení schematického výkresu a taková relaxace je pro ruční práci přirozená. Vytvářím grafy pomocí programu, takže takové potíže nemám, zde je poměrně přesný obrázek:

Přímé jsou vertikální asymptoty pro graf této funkce.
Odpovědět: funkce je spojitá na celé číselné ose kromě bodů, ve kterých trpí nespojitostmi 2. druhu.
Jednodušší funkce, kterou můžete vyřešit sami:
Příklad 9
Prozkoumejte spojitost funkce a vytvořte schematický nákres.
Přibližný příklad řešení na konci, které se nepozorovaně připlížilo.
Brzy se uvidíme!
Řešení a odpovědi:
Příklad 3:Řešení
: transformovat funkci: ![]() . S ohledem na pravidlo zpřístupnění modulu
. S ohledem na pravidlo zpřístupnění modulu ![]() a skutečnost, že , přepíšeme funkci po částech:
a skutečnost, že , přepíšeme funkci po částech:

Prozkoumejme funkci pro spojitost.
1) Funkce není v bodě definována .

Jednostranné limity jsou konečné a různé, což znamená, že funkce trpí diskontinuitou 1. druhu se skokem v bodě . Udělejme nákres:

Odpovědět: funkce je spojitá na celé číselné ose kromě bodu , ve kterém trpí diskontinuitou prvního druhu se skokem. Skoková mezera: (o dvě jednotky výše).
Příklad 5:Řešení
: Každá ze tří částí funkce je spojitá na svém vlastním intervalu.
já)
1)
2) Vypočítejme jednostranné limity:

![]() , což znamená, že existuje obecný limit.
, což znamená, že existuje obecný limit.
3)
![]() - limita funkce v bodě je rovna hodnotě této funkce v daném bodě.
- limita funkce v bodě je rovna hodnotě této funkce v daném bodě.
Takže funkce spojitý v bodě definováním spojitosti funkce v bodě.
II)
Zkoumáme bod pro spojitost
1) - funkce je definována v daném bodě. funkce trpí diskontinuitou 2. druhu v bodě
Jak najít doménu funkce?
Příklady řešení
Pokud někde něco chybí, znamená to, že někde něco je
Pokračujeme ve studiu části „Funkce a grafy“ a další stanice na naší cestě je Funkční doména. Aktivní diskuse o tomto konceptu začala v první lekci o funkčních grafech, kde jsem se podíval na elementární funkce, a zejména na jejich definiční domény. Proto doporučuji figurínům začít se základy tématu, protože se nebudu znovu zdržovat některými základními body.
Předpokládá se, že čtenář zná definiční obory základních funkcí: lineární, kvadratické, kubické funkce, polynomy, exponenciála, logaritmus, sinus, kosinus. Jsou definovány na . U tečen, arcsinus, budiž, odpouštím =) Vzácnější grafy se hned tak nepamatují.
Rozsah definice se zdá být jednoduchý a nabízí se logická otázka: o čem článek bude? V této lekci se podívám na běžné problémy hledání definičního oboru funkce. Navíc budeme opakovat nerovnosti s jednou proměnnou, jehož řešitelské dovednosti budou vyžadovány i v jiných úlohách vyšší matematiky. Materiál je mimochodem veškerý školní materiál, takže bude užitečný nejen pro studenty, ale i pro studenty. Informace se samozřejmě netváří encyklopedicky, ale zde nejsou přitažené „mrtvé“ příklady, ale pečené kaštany, které jsou převzaty ze skutečných praktických prací.
Začněme rychlým ponorem do tématu. Krátce k tomu hlavnímu: mluvíme o funkci jedné proměnné. Jeho doménou definice je mnoho významů "x", pro který existovat významy „hráčů“. Podívejme se na hypotetický příklad: 
Oblastí definice této funkce je sjednocení intervalů:
(pro ty, kteří zapomněli: - ikona sjednocení). Jinými slovy, pokud vezmete jakoukoli hodnotu „x“ z intervalu , nebo z , nebo z , pak pro každé takové „x“ bude hodnota „y“.
Zhruba řečeno, tam, kde je definiční obor, existuje graf funkce. Ale půlinterval a bod „tse“ nejsou zahrnuty v oblasti definice, takže tam není žádný graf.
Ano, mimochodem, pokud by z terminologie a/nebo obsahu prvních odstavců něco nebylo jasné, je lepší se k článku vrátit Grafy a vlastnosti elementárních funkcí.


