Základné pojmy a definície:
Nula analytickej funkcie f(z) je bod „a“, pre ktorý f(a)=0.
Nula rádu „n“ funkcie f(z) je bod „a“, ak fn(a)¹0.
Singulárny bod „a“ sa nazýva izolovaný singulárny bod funkcie f(z), ak existuje okolie tohto bodu, v ktorom nie sú žiadne iné singulárne body ako „a“.
Existujú tri typy izolovaných singulárnych bodov: .
1 odnímateľné singulárne body;
3 v podstate singulárne body.
Typ singulárneho bodu možno určiť na základe správania sa danej funkcie v nájdenom singulárnom bode, ako aj z tvaru Laurentovho radu získaného pre funkciu v okolí nájdeného singulárneho bodu.
Určenie typu singulárneho bodu podľa správania funkcie v ňom.
1. Odnímateľné singulárne body.
Izolovaný singulárny bod a funkcie f(z) sa nazýva odstrániteľný, ak existuje konečná limita.
2.Poliakov.
Izolovaný singulárny bod a funkcie f(z) sa nazýva pól if 
.
3. V podstate singulárne body.
Izolovaný singulárny bod a funkcie f(z) sa nazýva v podstate singulárny bod, ak neexistuje ani konečný, ani nekonečný.
Medzi nulami a pólmi funkcie existuje nasledujúci vzťah.
Aby bol bod a pólom rádu n funkcie f(Z), je potrebné a postačujúce, aby bol tento bod nulou rádu n pre funkciu .
Ak n=1 pól sa nazýva jednoduchý.
Definícia: Izolovaný singulárny bod jednoznačnej povahy sa nazýva:
a) odstrániteľné, ak chýba hlavná časť rozkladu;
b) pól, ak hlavná časť obsahuje konečný počet členov;
c) v podstate singulárny bod, ak hlavná časť obsahuje nekonečný počet členov.
a) V blízkosti odstrániteľného singulárneho bodu má teda rozšírenie tvar:
vyjadruje funkciu vo všetkých bodoch kružnice |z-a| V strede z=a rovnosť nie je pravdivá, pretože funkcia v z=a má diskontinuitu a pravá strana je spojitá. Ak sa zmení hodnota funkcie v strede, pričom sa rovná hodnote pravej strany, medzera sa odstráni - odtiaľ názov - odstrániteľná. b) V blízkosti pólu rádu m má rozšírenie Laurentovho radu tvar: c) V blízkosti jednoduchého pólu Zrážky a vzorce na ich výpočet. Zvyšok analytickej funkcie f(z) v izolovanom singulárnom bode z 0 je komplexné číslo rovné hodnote integrálu Zvyšok funkcie f(z) v izolovanom singulárnom bode z 0 je označený symbolom Res f(z 0) alebo Res (f(z); z 0). teda Rozlíšenie f(z 0)= Ak do vzorca (22.15.1) dáme n=-1, dostaneme: C-1 = alebo Res f(z 0)= C-1, tie. zvyšok funkcie f(z) vzhľadom na singulárny bod z 0 sa rovná koeficientu prvého člena so záporným exponentom v expanzii funkcie f(z) v Laurentovom rade. Výpočet zrážok. Pravidelné alebo odnímateľné singulárne body. Je zrejmé, že ak z=z 0 je pravidelný alebo odstrániteľný singulárny bod funkcie f(z), potom Res f(z 0)=0 (Laurentova expanzia v týchto prípadoch nemá hlavnú časť, takže c-1=0) . Poliak. Nech bod z 0 je jednoduchý pól funkcie f(z). Potom má Laurentov rad pre funkciu f(z) v blízkosti bodu z 0 tvar: Odtiaľ Preto prechodom tejto rovnosti do limity v z --z 0 dostaneme Rozlíšenie f(z0)= V podstate špeciálny bod. Ak je bod z 0 v podstate singulárny bod funkcie f(z), potom na výpočet zvyšku funkcie v tomto bode sa zvyčajne priamo určí koeficient c-1 v Laurentovom rade funkcie. Klasifikácia udalostí. Súčet, súčin udalostí, ich vlastnosti, grafické znázornenie. Udalosti sú rozdelené na: 1. Náhodný 2. Spoľahlivý 3. Nemožné Spoľahlivá je udalosť, ktorá nevyhnutne nastáva za daných podmienok (noc nasleduje ráno). Náhodná udalosť je udalosť, ktorá sa môže, ale nemusí stať (absolvovanie skúšky). Nemožná udalosť je udalosť, ktorá za daných podmienok nenastane (vytiahnutie zelenej ceruzky zo škatuľky len s červenými). Nechaj zq je singulárny bod funkcie /(r), t.s. f(z) ale v tomto bode je analytický (najmä v ňom nemusí byť definovaný). Ak je tam takéto prepichnuté okolie bodu zq (t. j. množina O z - zq f(z) je teda aialitický zo volal izolovaný singulárny bod funkcie f(z). Táto definícia zostáva rovnaká aj v prípade zn = oo, ak je jód prepichnutý blízkosťou bodu zq = oo rozumieť množine z> ja -
vonkajšok kruhu s jeho stredom v počiatku. Inými slovami, špeciálny bod zq sa považuje za izolované, ak existuje okolie tohto bodu, v ktorom je ist iných singulárnych bodov iných ako zq. V nasledujúcom texte uvažujeme iba singulárne body jedinečného charakteru (funkcia f(z) predpokladá sa, že sú jednoznačné). V závislosti od správania funkcie f(z) pri z -> zq Existujú tri typy singulárnych bodov. Izolovaný singulárny bod zq funkcie f(z) s názvom: 1) odnímateľný singulárny bod, ak existuje konečná hranica 2) pól, ak existuje limit 3) v podstate zvláštny bod, Ak f(z) nemá ani konečnú, ani nekonečnú limitu z-> zq. Príklad 26.1. Ukážme, že všetky tri typy singulárnych bodov sú realizované. Uvažujme f(z)= Bod zq = 0 je izolovaný špeciálny bod tejto funkcie. Pomocou vzorca (22.12) získame expanziu z čoho vyplýva, že existuje lim fi(z)= 1. Preto zq = 0 je je odnímateľný singulárny bod funkcie fi(z). Funkcia f‘j(z) =---má na hrote tyč zo= 1 pretože 2
r" X Pozrime sa teraz na funkciu )z(z)= e 1 ^ r a ukážte, že zo = O je v podstate singulárny bod tejto funkcie. Pri snažení z na nulu pozdĺž reálnej osi ľavý a pravý limit funkcie /z (z) rozdielne: lim s 1 / 1
=
0, lim s 1 /* = os. to znamená, x->0-0 x->0+O Čo f:i(z) nemá ani konečnú ani nekonečnú hranicu na 2 ->
Oh, to je. zq = O je v podstate singulárny bod tejto funkcie. (Všimnite si, že ako pointa zvykne z - iy na nulu pozdĺž funkcie imaginárnej osi nemá žiadny limit.) Existujú samozrejme neizolované singulárne body. Napríklad. funkcia má póly v bodoch z n = -, P= ±1, ±2,... teda Zq = 0 je neizolovaný singulárny bod tejto funkcie: v akomkoľvek (bez ohľadu na to, ako malom) okolí tohto bodu sú ďalšie singulárne body g str.
Nechaj zo- konečný izolovaný singulárny bod funkcie f(z). Potom f(z) je podobný v niektorom prepichnutom okolí bodu 0 Zo zo toto okolie možno považovať za kruh s vnútorným polomerom r = 0. Podľa vety 25.1 v posudzovanom okolí funkcia f(z) možno rozšíriť na sériu Laurent (25.2). Ukážeme, že správanie funkcie na 2 -> zq (t. j. typ singulárneho bodu zo) závisí od typu hlavnej časti rozšírenia (25.2); Táto okolnosť vysvetľuje pôvod termínu „hlavná časť“. Veta 2G.2. Izolovaný singulárny bod zo funkcie f(z) je odstrániteľný vtedy a len vtedy, ak má Lorapovova expanzia v punktovanom okolí tohto bodu oid tie. pozostáva len zo správnej časti, a všetky koeficienty hlavnej časti sa rovnajú odrážke. Dôkaz. 1. Nechajte zo- odnímateľný singulárny hrot. Dokážme, že Laurentovo rozšírenie funkcie f(z) má tvar (26.1). Od špeciálneho bodu zo odnímateľný, potom je tu konečný limit lim f(z) = A. teda f(z) je ohraničený v nejakom punktovanom okolí bodu 0 z - zq zo, tie. )(z) pre každého z z tejto blízkosti. Vezmime si hocijakú R. U р /?| a použite vzorce (25.3) pre koeficienty Laurentovho radu: Pre koeficienty hlavnej časti expanzie n =- 1,-2,... Za takéto hodnoty P máme p~ p-e 0 at R-> 0. Keďže hodnota R môže byť zvolený ľubovoľne malý, potom pán~" môžu byť také malé, ako chcete. Keďže |s t,| ^ pán~p a c„ nezávisia od p, potom c„ = 0 at A= - 1, -2,..., čo bolo potrebné dokázať. 2. Predpokladajme teraz, že Laurentova expanzia má tvar (26.1). Rad (26.1) je mocninný rad a. preto sa zbieha nielen v prepichnutej oblasti, ale aj v celom okolí z-zq vrátane bodu zo; jeho množstvo S(z) je analytický pri z a S(z)= )(z) pri 0 z - zo R. Preto existuje konečná hranica )(z)= Pt 5(g) = 5(th) - Preto singulárny bod zq Z->Zo Z-*Zo odnímateľné. Veta je dokázaná. Komentujte. Z dôkazu vety vyplýva, že v punktovanom okolí 0 z - zo odstrániteľného singulárneho bodu funkcia f(z) sa zhoduje s funkciou 5(r), ktorá je analytická v celom okolí z - zo. Ak teda dáme /(th) = S(zq), potom bez zmeny funkčných hodnôt f(z) v ľubovoľných bodoch prepichnutého okolia urobíme túto funkciu analytickou v Go, t.j. Poďme túto funkciu „odstrániť“. To vysvetľuje pojem „odnímateľný prvok“. Je prirodzené, že takéto body považujeme za pravidelné a nie singulárne body funkcie f(z).
Zvážte napríklad funkciu V príklade 26.1 sa ukázalo, že Pm Nr) = 1. t.j. singulárny bod zq = 0 odstrániteľné. Nastavením /i(0) = 1 odstránime singularitu a získame funkciu, ktorá je v bode analytická zq = 0 (a v celej rovine C). Poďme teraz charakterizovať póly z hľadiska Laurentových expanzií. Veta 26.3. Izolovaný singulárny bod Zo funkcie f(z) je pól práve vtedy, keď hlavná časť Laurentovej expanzie so stredom Zq má len konečný počet zreteľných z nulových koeficientov s n: Dôkaz. 1. Nechajte zq - pól, t.j. lim/( z) = oo. Dokážme, že Laurentovo rozšírenie funkcie f(z) má tvar (2G.2). Keďže lim f(z)= oo. potom je tu prepichnuté okolie bodu ki zq. kde f(z) je analytický a nemá žiadne nuly. Potom funkcia g(z) = 1 /f(z) bude tiež analytický v tejto prerazenej štvrti a lim g(z)= 0. Preto Zo je odnímateľný *-? *0 singulárny bod funkcie g(z). Poďme definovať g(z) v bode zo, uvedenie g(zo)=
0. Potom g(z) sa stanú analytickými v celom okolí (neprepichnutého) bodu z 0 , a z 0 bude jeho izolovaná nula. Označme podľa N násobnosť (poradie) tejto nuly. Ako bolo uvedené v §23, v susedstve bodu funkcia zq g(z) môžu byť zastúpené vo forme (pozri (23.2)) a (z$) f 0 a y>(z) je analytický v určitom susedstve bodu zo- Pretože ip(z) súvislý v bode zo A g>(zo) Ф 0" potom ip(z) nemá žiadne nuly v niektorom okolí tohto bodu. Preto funkcia 1 /-p(z) bude tiež analytický v tomto susedstve, a preto sa v ňom rozširuje v sérii Taylor: Otvorením zátvoriek a zmenou označenia koeficientov zapíšeme do formulára posledné rozšírenie kde c_jv = 1>o f 0. Hlavná časť Laurentovho rozšírenia funkcie /(r) teda obsahuje len konečný počet členov; dospeli sme k požadovanej rovnosti (26.2). 2. Nechajte v prerazenom okolí bodov th funkciu )(z) je reprezentovaná Laurentovou expanziou (26.2) (podrobnejšiu formu pozri (26.3)), ktorej hlavná časť obsahuje len konečný počet členov a s- d" f 0. To je potrebné dokázať Zq - funkčný pól f(z). Násobenie rovnosti (26.3) o (G - G o) iV , dostaneme funkciu Rad v (26.4) je mocninný rad, ktorý konverguje k analytickej funkcii nielen v punktovanom bode, ale aj v celom okolí bodu. Zq. Preto funkcia h(z) sa v tomto susedstve stane analytickým, ak ho ďalej zadefinujeme vložením h(zo)= s_dg f 0. Potom Bod th je teda pól a veta 26.3 je dokázaná. Násobnosť (poradie) nulovej funkcie g(z)= 1//(g) sa nazýva pólový poriadok funkcie /(r). Ak N- poradie pólu th, teda g(z)= (g - Zo) N ip(z), a choď) F 0, a ako je uvedené v prvej časti dôkazu vety 26.3, rozšírenie funkcie /(r) má tvar (26.3), kde c_/v f 0. Naopak, ak sa /(r) rozšíri do radu (26.3) a e-i F 0, teda t.s. N- poradie pólu funkcie /(r). teda pólové poradie funkcie zq/(G) sa rovná číslu najvyššieho nenulového koeficientu hlavnej časti Laurentovej expanzie v punktovanom okolí bodu zq(t. j. rovné tomuto číslu N,čo s_dg f 0 a Sp= 0 at P > N). Dokážme nasledujúce tvrdenie, ktoré je vhodné pre aplikácie. Dôsledok 26.4. Bod zq je pólom rádu N fikcie/(G) vtedy a len vtedy/(G) reprezentovateľné vo forme kde h(z) je analytická funkcia v blízkosti bodu th a h(zo) f 0. Dôkaz. Funkcia cp(z) = l/h(z) je analytický v určitom susedstve bodu h. Podmienka Dôsledku 26.4 je ekvivalentná nasledujúcemu: Preto zq -
nulová multiplicita N funkcie g(z). a teda pól mnohosti N funkcie /(2). II Príklad 26.5. Nájdite izolované singulárne body funkcie Riešenie: Body, v ktorých (z 2
+ 1 )(z+ Z) 2 = 0. Ak z 2
L- 1 = 0, potom 2 = ±g Ak (z 4-3) 2 = 0, teda z= -3. Preto má funkcia tri singulárne body z= g, 22 = -g, Z3
=
- 3. Zvážte z: G - pole prvého rádu (použili sme dôsledok 26.4). Podobným spôsobom sa dá dokázať, že 22 = -i aj pól prvého poriadku. Pre 2z máme: Prejdime k uvažovaniu v podstate singulárnych bodov. Veta 26.6. Izolovaný singulárny bod zq funkcie f(z) je v podstate singulárny vtedy a len vtedy, ak hlavná časť Laurentovho rozšírenia so stredom zq má nekonečne veľa odlišných od. nula, koeficienty od p. Dôkaz. Veta 26.6 priamo vyplýva z viet 26.2 a 26.3. Skutočne, ak bod zq je v podstate špeciálny, potom hlavná časť Laurentovho rozšírenia nemôže chýbať ani obsahovať konečný počet členov (inak bod Zq bude buď odnímateľný alebo tyčový). Preto musí byť počet členov v hlavnej časti nekonečný. Naopak, ak hlavná časť obsahuje nekonečne veľa pojmov, potom Zq nemôže byť ani odnímateľný bod, ani tyč. Z toho vyplýva, že tento bod je v podstate špeciálny. V podstate singulárny bod sa podľa definície vyznačuje tým, že funkcia /(2) nemá ani konečnú, ani nekonečnú limitu pre z ->zq. Úplnejšiu predstavu o tom, aké nepravidelné je správanie funkcie v susedstve v podstate singulárneho bodu, poskytuje nasledujúca veta. Veta 26.7 (Sochotského veta). Ak je zq pre jednotlivcov podstatný, bod funkcie f(z), potom pre ľubovoľné komplexné číslo L, vrátane A = oh, existuje postupnosť bodov z n taká, že z n -> zo a lim f(zn) = A. n->os Dôkaz. Pozrime sa najprv na prípad A = oo V prvej časti dôkazu vety 2G.2 sme zistili, že ak f(z) je ohraničený v nejakom punktovanom okolí bodu r, potom všetky koeficienty c", n = - 1,- 2,... hlavnej časti sa rovnajú nule (a teda singularita in go je odstrániteľná). Keďže podľa podmienky th je esenciálny singulárny bod, potom v akomkoľvek punktovanom okolí bodu th je funkcia f(r) neobmedzená. Zoberme si nejaké silné okolie 0 Z také, že f(zi) > 1 (ak |/(r)| z - zo I/2 je tam bodka z-2
, v ktorom |/(yy)| > 2 atď.: v prepichnutom okolí O 71.
Je zrejmé, že r„ -e ísť a lim /(r“) = oo. Teda v prípade A = oo platí Veta 26.7 osvedčené. Nechaj to teraz A f oo Najprv predpokladajme, že existuje prepichnutá oblasť 0 = -yy----
bude analytický v tejto prerazenej štvrti a následne /(G) - A V dôsledku toho je go izolovaný singulárny bod funkcie Φ(r). Ukážeme vám to. že r je v podstate singulárny bod Φ(r). To nemusí byť pravda. Potom existuje limita lim Ф(r), konečná alebo nekonečná. Na chvíľu /(r) = A + , potom je tu aj Hsh /(r), čo je v rozpore s podmienkou F(g)~ :-*z 0 Vidím vetu. r0 je teda v podstate singulárny bod funkcie Φ(r). Podľa toho, čo bolo dokázané vyššie, existuje postupnosť bodov r n taká, že r n-tá a lim Ф(r n) = oo. Odtiaľ Dokázali sme požadované vyhlásenie za predpokladu, že /(r) F A v nejakom prepichnutom okolí bodu cho- Predpokladajme teraz, že toto je nepravdivé, t.j. v ľubovoľnom malom prerazenom okolí bodu th je taký bod G",že /(r") = L. Potom pre ľubovoľné P v punktovanom okolí 0 f(z u) = А Požadované tvrdenie je teda pravdivé P-yu vo všetkých prípadoch a veta 26.7 je dokázaná. Podľa vety 26.7 (Sokhotsky) v akomkoľvek (ľubovoľne malom) punktovanom okolí v podstate singulárneho bodu funkcia /(r) nadobúda hodnoty ľubovoľne blízke akémukoľvek číslu z rozšírenej komplexnej roviny C. Na štúdium izolovaných singulárnych bodov sú často užitočné už známe Taylorove expanzie základných elementárnych funkcií. Príklad 2G.8. Určte typ singulárneho bodu zq = 0 funkcie Vyriešené a e Rozšírme čitateľa a menovateľa na Taylorov rad v mocninách g z namiesto r a odčítaním 1 dostaneme Pomocou (22.12) dostaneme rozšírenie menovateľa: Séria v týchto rozšíreniach sa zbieha v celej komplexnej rovine €. Máme a /2(2) sú anaritické v susedstve bodu zo = 0 (a dokonca v celej rovine) a /2 (20) F 0, teda h(z) je tiež analytický v určitom okolí bodu hF 0. Podľa záveru 26.4 bod Zo = 0 je pól poriadku N=4. II Príklad 26.9. Nájdite singulárne body funkcie f(z)= hriech j - a určte ich druh. R e v e i e Funkcia má jeden konečný singulárny bod zq = 1. V ostatných bodoch od C funkcia w =--- analytické; teda funkcia sin w bude analytický. Dosadením v expanzii sínusu (22.12) - namiesto r dostaneme Získali sme rozšírenie funkcie sin do Laurentovho radu v punktovanom okolí bodu 2o = 1. Keďže výsledný rozvoj obsahuje nekonečne veľa členov so zápornými mocninami (r - 1), potom zq = 1 je v podstate singulárny bod (v tomto prípade Laurentova expanzia pozostáva len z hlavnej časti a pravidelná časť chýba). Všimnite si, že v tomto prípade bolo možné určiť povahu singularity priamo z definície bez použitia rozšírenia série. V skutočnosti existujú sekvencie (r") a (2"), ku ktorým sa zbiehajú zo= 1 a také, že f(z"n)= 1, /(2") = 0 (takéto sekvencie uveďte sami). f(z) nemá žiadne obmedzenie z -> 1 a teda bod zq - 1 je v podstate špeciálny. Predstavme si koncept Laurentovho rozšírenia funkcie v okolí bodu Zq = 00 a zvážte súvislosť medzi expanziou a povahou singularity v tomto bode. Všimnite si, že definície izolovaného singulárneho bodu a jeho typ (odnímateľný, pólový alebo v podstate singulárny) sa prenášajú do prípadu zq = oc bez zmien. Ale vety 26.2. 26.3 a 26.6, ktoré súvisia s charakterom Laurentových rozšírení, je potrebné zmeniť. Ide o to, že členovia cn(z- 2o) str. P= -1,-2,..., hlavná časť, definujúca „nepravidelnosť“ funkcie v blízkosti koncového bodu Zq, keďže 2 má tendenciu oo, budú sa správať „správne“ (smerne k 0). Naopak, členovia správnej časti s P= 1,2,... bude mať tendenciu oo; určujú povahu funkcie v Zq = oo. Preto hlavná časť expanzie v okolí oo bude pozostávať z pojmov s pozitívnymi právomocami P, a ten správny - s negatívnymi. Predstavme si novú premennú w = 12. Funkcia tv = 1/2, rozšírené tak, že u(oo) = 0, jedna k jednej a konformne mapuje okolie z > R bodov zq = 00 v blízkosti |w| wq = 0. Ak funkcia f(z) analýzy v prepichnutej štvrti R z Zq = oc, potom funkcia G(w) = f(l/w) bude analytický vo veľkom susedstve 0 wo = 0. Keďže pri 2 -> oo bude w-> 0 teda Preto G(w) má v bode wq = 0 je vlastnosť rovnakého typu ako f(z) v bode Zq = 00. Rozšírme funkciu G(w) na Laurentov rad v punktovanom okolí bodu wo = 0: Súčty na pravej strane (26.5) predstavujú pravidelné a hlavné časti expanzie. Prejdime k premennej z, nahrádzanie w = 1/z: Určenie P= -A*, 6* = 6_„= s p a všímať si to G(l/z) = f(z), dostaneme Rozklad (2G.G) sa nazýva Laurentov rozvoj funkcie f(z) v punktovanom okolí bodu zq= oo. Volá sa prvý súčet v (2G.6). pravá časť, a druhá suma je Hlavná časť tohto rozkladu. Keďže tieto súčty zodpovedajú správnym a hlavným častiam rozšírenia (26.5), potom pre rozšírenie (26.6) platia analógy viet 26.2, 26.3 a 26.6. Nasledujúca veta bude teda analógom vety 26.2. Veta 26.10. Izolovaný singulárny bodZq -
OS (funkcie/(G) je odstrániteľná vtedy a len vtedy, ak Laurentova expanzia v prepichnutom okolí tohto bodu má tvar
t.s. pozostáva len zo správnej časti. Dajme /(oo) = spol. Funkcia definovaná radom (26.7) konvergujúcim v okolí z > R bod 2о = oc, tzv analytický v bode z o = oo. (Všimnite si, že táto definícia je ekvivalentná s analytikou funkcie G(w) v bode wo = 0.) Príklad 26.11. Preskúmajte singulárny bod zq = oo funkcie Keďže je limit konečný zo = oo je odstrániteľný singulárny bod funkcie /(r). Ak dáme /(oo) = lim J(z)= 0 teda f(z) sa stane analytickým tik na mieste Zo= os. Ukážme, ako nájsť zodpovedajúce rozšírenie (26.7). Prejdime k premennej w = 1 fz. Nahrádzanie z= 1 /?е, dostaneme (posledná rovnosť platí v punktovanom okolí bodu w® = 0, ale budeme ďalej definovať (7(0) = 0). Výsledná funkcia má singulárne body w =±i, w =-1/3 a v bode Wq = 0 je analytický. Funkcia rozkladania G(w) podľa stupňov w(ako bolo urobené v príklade 25.7) a dosadením do výsledného mocninového radu w = 1/z, môžeme získať expanziu (26.7) funkcie f(z).
Veta 26.3 pre prípad zo= oo sa prepíše do nasledujúcej podoby. Veta 26.12. Izolovaný singulárny bod th = os funkcia f(z) je pól práve vtedy, ak je hlavnou časťou Laurentovho rozšírenia (26.6) má len konečný počet nenulových koeficientov S": Tu je séria pravidelná časť a polynóm v zátvorkách je hlavnou časťou rozšírenia. Pólová multiplicita v oc je definovaná ako pólová multiplicita wq = 0 funkcií G(z). Je ľahké vidieť, že početnosť pólu sa zhoduje s číslom N v (26.8). Q p | (i 2 + 1) (z + 3) 2 Úloha. Ukážte, že funkcia f(z) =--
-- má v bod zo = oo pól poriadku 3. Veta 26.6 o v podstate singulárnom bode môže byť pre tento prípad prepísaná zo= os takmer doslovne a my sa tým podrobne nezaoberáme. Taylorov rad slúži ako efektívny nástroj na štúdium funkcií, ktoré sú analytické v kruhu zol Na štúdium funkcií, ktoré sú analytické v kruhovej doméne, sa ukazuje, že je možné zostrojiť expanzie v kladných a záporných mocninách (z - zq) tvaru. ktoré zovšeobecňujú Taylorove expanzie. Séria (1), chápaná ako súčet dvoch sérií, sa nazýva Laurentova séria. Je zrejmé, že oblasť konvergencie radu (1) je spoločnou časťou oblastí konvergencie každého radu (2). Poďme ju nájsť. Oblasť konvergencie prvého radu je kruh, ktorého polomer je určený Cauchyho-Hadamardovým vzorcom Vo vnútri kruhu konvergencie séria (3) konverguje k analytickej funkcii a v akomkoľvek kruhu s menším polomerom konverguje. absolútne a jednotne. Druhý rad je mocninný rad vzhľadom na premennú Rad (5) konverguje v rámci svojho kruhu konvergencie k analytickej funkcii komplexnej premennej m-*oo a v ľubovoľnom kruhu menšieho polomeru konverguje absolútne a rovnomerne. znamená, že oblasť konvergencie radu (4) je vonkajšok kruhu - Ak potom existuje spoločná oblasť konvergencie radu (3) a (4) - kruhový kruh, v ktorom séria (1) konverguje k analytickej funkcii. Navyše v akomkoľvek kruhu konverguje absolútne a rovnomerne. Príklad 1. Určite oblasť konvergencie Rad Laurentovho radu Izolované singulárne body a ich klasifikácia M Oblasť konvergencie prvého radu je vonkajšok kružnice a oblasť konvergencie druhého radu je vnútro kružnice. tento rad konverguje do kružníc Veta 15. Akákoľvek funkcia f (z), jednoznačná a apolitická v kruhovom kruhu, môže byť reprezentovaná v tomto kruhu ako súčet konvergentného radu, ktorého koeficienty Cn sú jednoznačne určené a vypočítané podľa vzorcov kde 7p je kružnica s polomerom m. Upevnime ľubovoľný bod z vo vnútri kruhu R. Zostrojme kružnice so stredmi v bode r, ktorých polomery vyhovujú nerovnostiam a uvažujme nový kruh Pomocou Cauchyho integrálnej vety pre násobne spojenú oblasť máme Transformujeme samostatne každý z integrálov v súčte (8). Pre všetky body £ pozdĺž kružnice 7d* je splnený vzťah de sum rovnomerne konvergentného radu 1 1. Preto zlomok ^ môžeme reprezentovať vo vi- / "/ vynásobením oboch častí spojitou funkciou (O a vykonaním. integráciou po členoch po kružnici dostaneme, že transformáciu druhého integrálu vykonáme trochu inak. Pre všetky body £ na kružnici ir> teda platí zlomok ^ ako súčet rovnomerne konvergentných radov vynásobením oboch častí spojitou funkciou) a integráciou po kružnici 7/ dostaneme, že integrandy vo vzorcoch (10) a (12) sú analytické funkcie v kruhovom kruhu. Preto sa na základe Cauchyho vety hodnoty príslušných integrálov nezmenia, ak kruhy 7/r a 7r/ nahradíme ľubovoľným kruhom. To nám umožňuje kombinovať vzorce (10) a (12) Nahradením integrálov na pravej strane vzorca (8) ich výrazmi (9) a (11), pretože z je ľubovoľné bod kruhu, z toho vyplýva, že rad ( 14) konverguje k funkcii f(z) všade v tomto kruhu a v ktoromkoľvek kruhu rad konverguje k tejto funkcii absolútne a rovnomerne. Dokážme teraz, že rozklad tvaru (6) je jedinečný. Predpokladajme, že existuje ešte jedna expanzia. Potom všade vo vnútri kruhu R budeme mať na kružnici rad (15) rovnomerne konvergovať. Vynásobme obe strany rovnosti (kde m je pevné celé číslo a integrujme oba členy v rade členmi. Výsledkom je, že na ľavej strane a na pravej strane dostaneme Sch. Teda (4, = sv. m je ľubovoľné číslo, posledná rovnosť dokazuje jedinečnosť radu (6), ktorého koeficienty sú vypočítané pomocou vzorcov (7), nazývame Laurentovým radom funkcie f(z) v kruhu súbor termov tohto radu s nezápornými mocninami sa nazýva správna časť Laurentovho radu a so zápornými - jeho hlavná časť Vzorce (. 7) pre koeficienty Laurentovho radu sa v praxi používajú len zriedka, pretože pravidlo, vyžadujú ťažkopádne výpočty Zvyčajne, ak je to možné, sa použijú hotové Taylorove expanzie elementárnych funkcií, každá legitímna metóda vedie k rovnakému výsledku funkcií v rôznych oblastiach za predpokladu, že f(r) má dva singulárne body: Preto existujú tri kruhové oblasti so stredom v bode r = 0. v každej z nich je funkcia /(r) analytická: a. ) kruhový krúžok na vonkajšej strane kruhu (obr. 27). Nájdite Laurentove expanzie funkcie /(z) v každej z týchto oblastí. Predstavme /(z) ako súčet elementárnych zlomkov a) Kruh Vzťah (16) transformujeme nasledovne Pomocou vzorca pre súčet členov geometrickej postupnosti dosadíme nájdené expanzie do vzorca (17). : Toto rozšírenie je Taylorovým radom funkcie /(z). b) Kruh pre funkciu -r zostáva v tomto kruhu konvergentný, pretože séria (19) pre funkciu j^j pre |z| > 1 sa líši. Preto transformujeme funkciu /(z) nasledovne: opäť použitím vzorca (19) dostaneme, že tento rad konverguje pre. Dosadením expanzií (18) a (21) do vzťahu (20) dostaneme c) Vonkajší povrch kružnice pre funkciu -z pre |z| > 2 divergencie a rad (21) pre funkciu- Predstavme funkciu /(z) v nasledujúcom tvare: /<*> Pomocou vzorcov (18) a (19) dostaneme OR 1 Tento príklad ukazuje, že pre rovnakú funkciu f(z) má Laurentov expanzia, všeobecne povedané, rôzny tvar pre rôzne kruhy. Príklad 3. Nájdite rozšírenie 8. Laurentovho radu funkcie Laurentov rad Izolované singulárne body a ich zaradenie do kruhovej oblasti A Použijeme reprezentáciu funkcie f(z) v nasledujúcom tvare: a transformujeme druhý člen Pomocou vzorec pre súčet členov geometrickej postupnosti dostaneme Dosadením nájdených výrazov do vzorca (22) máme Príklad 4. Rozšírte funkciu v Laurentovom rade v oblasti zq = 0. Pre ľubovoľný komplex máme Nech toto expanzia platí pre ľubovoľný bod z Ф 0. V tomto prípade oblasť kruhu predstavuje celú komplexnú rovinu s jedným vyradeným bodom z - 0. Túto oblasť možno definovať nasledujúcim vzťahom: Táto funkcia je analytická v oblasti Zo vzorcov ( 13) pre koeficienty Laurentovho radu, použitím rovnakého uvažovania ako v predchádzajúcom odseku, možno získať Kouiwove nerovnosti. ak je funkcia f(z) ohraničená na kružnici, kde M je konštanta), potom Izolované singulárne body Bod zo sa nazýva izolovaný singulárny bod funkcie f(z), ak existuje kruhové okolie bodu ( táto množina sa niekedy nazýva punktované okolie bodu 2o, v ktorom je funkcia f(z) jedinečná a analytická. V samotnom bode zo je funkcia buď nedefinovaná, alebo nie je jednoznačná a analytická. V závislosti od správania sa funkcie /(r) pri priblížení sa k bodu zo sa rozlišujú tri typy singulárnych bodov. Izolovaný singulárny bod sa považuje za: 1) odstrániteľný, ak existuje konečný 2) pmusach, ak 3) v podstate singulárny bod, ak funkcia f(z) nemá limit na Typ izolovaného singulárneho bodu úzko súvisí s povaha Laurentovho rozšírenia funkcie prepichnutým stredom . Veta 16. Izolovaný singulárny bod z0 funkcie f(z) je odstrániteľný singulárny bod práve vtedy, ak Laurentova expanzia funkcie f(z) v okolí bodu zo neobsahuje hlavnú časť, t.j. má tvar Nech zo je odstrániteľný singulárny bod. Potom existuje konečnosť, preto je funkcia f(z) ohraničená v prokologickom okolí bodu z. Na základe Cauchyho nerovností, keďže p môžeme zvoliť ľubovoľne malé, potom sú všetky koeficienty v záporných mocninách (z. - 20) sa rovnajú nule: Naopak, nech Laurentov rozvoj funkcie /(r) v okolí bodu zq obsahuje len správnu časť, teda má tvar (23), a teda je Taylor. Je ľahké vidieť, že pre z -* z0 má funkcia /(z) limitnú hodnotu: Veta 17. Izolovaný singulárny bod zq funkcie f(z) je odstrániteľný vtedy a len vtedy, ak je funkcia J(z) ohraničený v nejakom prerazenom susedstve bodu zq, Zgmechai nie. Nech r je odstrániteľný singulárny bod funkcie /(r). Za predpokladu, že dostaneme, že funkcia /(r) je analytická v nejakej kružnici so stredom v bode r. To určuje názov bodu - odnímateľný. Veta 18. Izolovaný singulárny bod zq funkcie f(z) je pólom práve vtedy, ak hlavná časť Laurentovho rozšírenia funkcie f(z) v okolí bodu obsahuje konečné (a kladné) číslo nenulových členov, t.j. má tvar 4 Nech z0 je pól. Odvtedy existuje punktované okolie bodu z0, v ktorom je funkcia f(z) analytická a nenulová. Potom v tomto okolí je definovaná analytická funkcia a preto bod zq je odstrániteľný singulárny bod (nula) funkcie alebo kde h(z) je analytická funkcia, h(z0) Φ 0. Potom h(zo) Φ 0 je tiež analytická, potom je funkcia φ analytická v okolí bodu zq, a preto, odkiaľ to získame Predpokladajme teraz, že funkcia f(z) má expanziu tvaru (24) v punktovanom okolí bod zо. To znamená, že v tomto okolí je funkcia f(z) analytická spolu s funkciou. Pre funkciu g(z) platí expanzia, z ktorej je vidieť, že zq je odstrániteľný singulárny bod funkcie g(z) a potom funkcia v 0 má tendenciu byť pólom funkcie je ďalší jednoduchý fakt. Bod Zq je pólom funkcie f(z) vtedy a len vtedy, ak funkcia g(z) = уй môže byť rozšírená na analytickú funkciu v okolí bodu zq nastavením g(z0) = 0. pólu funkcie f(z) sa nazýva nultý rád funkcie jfa. Nasledujúce tvrdenie vyplýva z vety 16 a 18. Veta 19. Izolovaný singulárny bod je v podstate singulárny vtedy a len vtedy, ak hlavná časť Laurentovho rozšírenia v punktovanom okolí tohto bodu obsahuje nekonečne veľa nenulových členov. Príklad 5. Singulárny bod funkcie je zo = 0. Máme izolované singulárne body Laurentovho radu a ich klasifikáciu Preto zo = O je odstrániteľný singulárny bod. Rozšírenie funkcie /(z) do Laurentovho radu v blízkosti nulového bodu obsahuje iba správnu časť: Príklad7. /(z) = Singulárny bod funkcie f(z) je zq = 0. Uvažujme správanie sa tejto funkcie na reálnej a imaginárnej osi: na reálnej osi v x 0, na imaginárnej osi. nie je ani konečná, ani nekonečná limita pre f(z) v z -* 0 neexistuje. To znamená, že bod r = 0 je v podstate singulárny bod funkcie f(z). Nájdite Laurentovu expanziu funkcie f(z) v blízkosti nulového bodu. Pre akýkoľvek komplex C máme Set. Potom Laurentova expanzia obsahuje nekonečný počet členov so zápornými mocninami z. Singulárny bod v matematike. 1) Singulárny bod krivky definovaný rovnicou F ( x, y) = 0, - bod M 0 ( x 0, y 0), v ktorom obe parciálne derivácie funkcie F ( x, y) ísť na nulu: Ak nie všetky druhé parciálne derivácie funkcie F ( x, y) v bode M 0 sa rovnajú nule, potom sa O. t. Ak spolu s prvými deriváciami miznúcimi v bode M0 zmiznú aj všetky druhé derivácie, ale nie všetky tretie derivácie, potom sa rovnica nazýva trojitá atď. Pri štúdiu štruktúry krivky v blízkosti dvojitého O.t. zohráva významnú úlohu znak výrazu Ak Δ > 0, potom sa otvorený okruh nazýva izolovaný; napríklad pri zákrute y 2 - x 4 + 4 x 2= 0, počiatok súradníc je izolovaný O. t. ryža. 1
). Ak Δ x 2 + y 2 + a 2) 2 - 4a 2 x 2 - a 4= 0, počiatkom súradníc je uzol O. t. ryža. 2
). Ak Δ = 0, potom je všeobecný bod krivky buď izolovaný, alebo sa vyznačuje tým, že rôzne vetvy krivky majú v tomto bode spoločnú dotyčnicu, napr.: a) vrcholový bod 1. druhu - rôzne vetvy krivky krivky sú umiestnené na opačných stranách spoločnej dotyčnice a tvoria bod ako krivka y 2 - x 3= 0 (pozri ryža. 3
, a); b) vrcholový bod 2. druhu - rôzne vetvy krivky sú umiestnené na jednej strane spoločnej dotyčnice ako krivka
(y - x 2)2 - x 5= 0 (pozri ryža. 3
, b); c) samodotykový bod (pre krivku y 2 - x 4= 0 počiatok je bod vlastného dotyku; (cm. ryža. 3
, V). Spolu s naznačeným O. t je mnoho ďalších O. t. napríklad asymptotický bod je vrcholom špirály s nekonečným počtom závitov (pozri. ryža. 4
), koncový bod, rohový bod atď. 2) Singulárny bod diferenciálnej rovnice je bod, v ktorom súčasne zmizne čitateľ aj menovateľ pravej strany diferenciálnej rovnice (pozri Diferenciálne rovnice) kde P a Q sú spojito diferencovateľné funkcie. Za predpokladu, že sa O. t nachádza v počiatku súradníc a pomocou Taylorovho vzorca (pozri Taylorov vzorec), môžeme rovnicu (1) znázorniť v tvare kde P 1 ( x, y) a Q 1 ( x, y) - nekonečne malý vzhľadom na Konkrétne, ak λ 1 ≠ λ 2 a λ 1 λ 2 > 0 alebo λ 1 = λ 2, potom je O. t. vstupujú do nej všetky integrálne krivky prechádzajúce bodmi v dostatočne malom okolí uzla. Ak λ 1 ≠ λ 2 a λ 1 λ 2 i β, α ≠ 0 a β ≠ 0, potom je všeobecným bodom ohnisko; všetky integrálne krivky prechádzajúce bodmi v dostatočne malom okolí ohniska predstavujú špirály s nekonečným počtom závitov v ľubovoľne malom okolí ohniska. Ak napokon λ 1,2 = ± iβ, β ≠ 0, potom charakter O. t nie je určený iba lineárnymi členmi v expanziách P (. x, y) a Q ( x, y), ako tomu bolo vo všetkých vyššie uvedených prípadoch; tu O. t môže byť ohniskom alebo centrom, alebo môže mať zložitejší charakter. V blízkosti stredu sú všetky integrálne krivky uzavreté a obsahujú stred v sebe. Takže napríklad bod (0, 0) je uzlom pre rovnice pri" = 2u/x(λ 1 = 1, λ 2 = 2; pozri ryža. 5
, a) a r" = u/x(λ 1 = λ 2 = 1; pozri ryža. 5
, b), sedlo pre rovnicu y" = -y/x(λ1 = -1, λ2 = 1 ; cm. ryža. 6
), ohnisko rovnice y" =(x + y) /
(x - y) (λ 1 = 1 - iλ2 = 1+ i; cm. ryža. 7
) a stred rovnice y" = -x/y(λ 1 = -iλ2 = i; cm. ryža. 8
). Ak x, y) a Q ( x, y) analytické, okolie GP vyššieho rádu možno rozdeliť na oblasti: D 1 - vyplnené integrálnymi krivkami, obidva konce zahrnuté v GP (eliptické oblasti), D 2 - vyplnené integrálnymi krivkami, jeden koniec zahrnutý v GP (parabolické oblasti) a D3 - oblasti ohraničené dvoma integrálnymi krivkami zahrnutými vo všeobecnej teórii, medzi ktorými sa nachádzajú integrálne krivky hyperbolického typu (hyperbolické oblasti) (pozri. ryža. 9
). Ak v orbitálnom t nie sú zahrnuté žiadne integrálne krivky, potom sa orbitál t nazýva bod stabilného typu. Okolie stabilného oscilátora pozostáva z uzavretých integrálnych kriviek obsahujúcich v sebe osmózu, medzi ktorými sú špirály (pozri obr. ryža. 10
). Štúdium diferenciálnych rovníc, teda v podstate štúdium správania sa rodín integrálnych kriviek v okolí diferenciálnych rovníc, predstavuje jednu z oblastí kvalitatívnej teórie diferenciálnych rovníc a zohráva dôležitú úlohu v aplikáciách, najmä v otázky stability pohybu (diela A. M. Lyapunova a, A. Poincareho atď.). 3) Singulárny bod jednohodnotovej analytickej funkcie je bod, v ktorom je analyticita funkcie narušená (pozri Analytické funkcie). Ak je tu okolie O. t. a, voľný od iných O. t., potom bod A nazývaný izolovaný O. t A- izolovaná všeobecná teória a existuje konečné a sa nazýva odstrániteľná všeobecná teória Vhodnou zmenou definície funkcie v bode a (alebo jej predefinovaním v tomto bode, ak funkcia v nej nie je vôbec definovaná), totiž predpokladaním f(a)= b, je možné to dosiahnuť a sa stane obyčajným bodom opravenej funkcie. Napríklad bodka z= 0 je odstrániteľný O. t pre funkciu f 1 ( z) = f(z), Ak z≠ 0 a f 1 (0), = 1, bodka z= 0 je obyčajný bod [ f 1 (z) je v podstate analytický z= 0]. Ak A- izolovaný O. t a a sa nazýva pól alebo nepodstatne singulárny bod funkcie f(z), ak funguje Laurentov rad). f(z) v blízkosti izolovaného O. t z - a, Ak A- odnímateľný O. t., obsahuje konečný počet záporných stupňov z - a, Ak A- pól (v tomto prípade poradie pólu R je definovaný ako najvyšší stupeň a - v podstate špeciálny bod. Napríklad pre funkciu bodka z= 0 je pól poriadku R, za funkciu bodka z= 0 je v podstate singulárny bod. Na hranici kružnice konvergencie mocninného radu musí byť aspoň jeden DP funkcie reprezentovanej v tomto kruhu daným mocninným radom. Všetky hraničné body oblasti existencie jedinej analytickej funkcie (prirodzená hranica) sú hranicami tejto funkcie. Teda všetky body jednotkovej kružnice | z| = 1 sú špeciálne pre funkciu Pre viachodnotovú analytickú funkciu platí pojem „O. T." ťažšie. Okrem O. t. je v jednotlivých listoch Riemannovej plochy funkcie (t. j. O. t. jednohodnotových analytických prvkov) aj O. t. Izolované body vetvenia Riemannovej plochy (t. j. také body vetvenia, že v niektorom z nich nie sú v žiadnom liste iné O. t. funkcie) sú klasifikované nasledovne. Ak a je izolovaný bod vetvy konečného poriadku a existuje konečné a, nazýva sa kritický pól. Ak A- izolovaný odbočný bod nekonečného poriadku a sa nazýva transcendentálny O.t. Všetky ostatné izolované odbočné body sa nazývajú kritické v podstate singulárne body. Príklady: bodka z= 0 je obyčajný kritický bod funkcie f ( z) = log z a kritický v podstate singulárny bod funkcie f (z) = hriech ln z. Každá všeobecná teória, okrem odstrániteľnej, je prekážkou analytického pokračovania, to znamená, že analytické pokračovanie pozdĺž krivky prechádzajúcej neredukovateľným všeobecným problémom je nemožné. Veľká sovietska encyklopédia. - M.: Sovietska encyklopédia.
1969-1978
.
Body tu. Pozri tiež singulárny bod (diferenciálne rovnice). Vlastnosť alebo singularita v matematike je bod, v ktorom je matematický objekt (zvyčajne funkcia) nedefinovaný alebo má nepravidelné správanie (napríklad bod, v ktorom ... ... Wikipedia Analytická funkcia je bod, v ktorom sú porušené podmienky analytiky. Ak je analytická funkcia f(z) daná v určitom okolí bodu z0 všade... Fyzická encyklopédia Analytická funkcia je bod, v ktorom je porušená analyticita funkcie... Veľký encyklopedický slovník singulárny bod- - [Ya.N.Luginsky, M.S.Fezi Zhilinskaya, Yu.S.Kabirov. Anglicko-ruský slovník elektrotechniky a energetiky, Moskva, 1999] Témy elektrotechniky, základné pojmy EN jednotný bod ... Technická príručka prekladateľa 1) Analytická funkcia f(z) je prekážkou analytického pokračovania prvku funkcie f(z) komplexnej premennej z pozdĺž nejakej dráhy v rovine tejto premennej. Nech je analytická funkcia f(z) definovaná nejakým... ... Matematická encyklopédia Analytická funkcia, bod, v ktorom je narušená analytickosť funkcie. * * * JEDEN BOD JEDNODUCHÝ BOD analytickej funkcie, bod, v ktorom je narušená analytickosť funkcie... encyklopedický slovník singulárny bod- ypatingasis taškas statusas T sritis automatika atitikmenys: angl. jednotný bod vok. singulärer Punkt, m rus. singulárny bod, f pranc. bodový partikul, m; bod singulier, m … Automatikos terminų žodynas singulárny bod- ypatingasis taškas statusas T sritis fizika atitikmenys: angl. jednotný bod vok. singulärer Punkt, m rus. singulárny bod, f pranc. bod singulier, m … Fizikos terminų žodynas Modely opísané sústavami dvoch autonómnych diferenciálnych rovníc.
Fázová rovina. Fázový portrét. Izoklinická metóda. Hlavné izokliny. Stabilita stacionárneho stavu. Lineárne systémy. Typy singulárnych bodov: uzol, sedlo, ohnisko, stred. Príklad: chemické reakcie prvého rádu.
Najzaujímavejšie výsledky o kvalitatívnom modelovaní vlastností biologických systémov boli získané pomocou modelov dvoch diferenciálnych rovníc, ktoré umožňujú kvalitatívny výskum pomocou metódy fázová rovina. Uvažujme systém dvoch autonómnych obyčajných diferenciálnych rovníc všeobecného tvaru (4.1)
P(x,y), Q(x,y)- spojité funkcie definované v nejakej doméne G Euklidovská rovina ( x, y- karteziánske súradnice) a majúce v tejto oblasti spojité derivácie rádu nie nižšie ako prvé. región G môžu byť neobmedzené alebo obmedzené. Ak premenné x, y majú špecifický biologický význam (koncentrácie látok, počty druhov) najčastejšie oblasť G predstavuje kladný kvadrant pravej polroviny: 0
£
X<
¥
,0
£
r<
¥
.
Koncentrácie látok alebo počet druhov môžu byť tiež zhora obmedzené objemom nádoby alebo plochou biotopu. Potom má rozsah premenných tvar: 0
£
X< x 0 ,
0
£
r< y 0
.
Premenné x, y zmena v čase v súlade so systémom rovníc (4.1), takže každý stav systému zodpovedá dvojici premenných hodnôt ( x, y).
Naopak, každá dvojica premenných ( x, y) zodpovedá určitému stavu systému. Zvážte rovinu so súradnicovými osami, na ktorých sú vynesené hodnoty premenných x, y. Každý bod M táto rovina zodpovedá určitému stavu systému. Táto rovina sa nazýva fázová rovina a predstavuje súhrn všetkých stavov systému. Bod M(x,y) sa nazýva reprezentujúci alebo reprezentujúci bod.
Nechajte v počiatočnom okamihu t = t 0 súradníc reprezentujúceho bodu M 0 (X(t 0), r(t 0)).
V každom ďalšom okamihu t reprezentujúci bod sa bude posúvať v súlade so zmenami hodnôt premenných X(t), r(t).
Zber bodov M(X(t), y(t)) na fázovej rovine, ktorej poloha zodpovedá stavom systému v procese meniacich sa premenných v čase x(t), y(t) podľa rovníc (4.1), je tzv fázová trajektória.
Sada fázových trajektórií pre rôzne počiatočné hodnoty premenných poskytuje ľahko viditeľný „portrét“ systému. Stavebníctvo fázový portrét umožňuje vyvodiť závery o charaktere zmien premenných x, y bez znalosti analytických riešení pôvodnej sústavy rovníc(4.1).
Na zobrazenie fázového portrétu je potrebné zostrojiť vektorové pole smerov trajektórií systému v každom bode fázovej roviny. Nastavenie prírastkuD
t>0,dostaneme zodpovedajúce prírastky
D
X A D
r z výrazov: D
x=P(x,y)D
t,
D
y=Q(x,y)D
t. Vektorový smer dy/dx v bode ( x, y) závisí od znamienka funkcií P(x, y), Q(x, y) a môže byť daný tabuľkou: P(x,y)>0,Q(x,y)>0 P(x,y)<0,Q(x,y)<0
P(x,y)>0,Q(x,y)<0
P(x,y)<0,Q(x,y)>0
.(4.2)
Riešenie tejto rovnice
y = y(x,c),
alebo implicitne F(x, y)=c, Kde s– integračná konštanta, dáva rodinu integrálnych kriviek rovnice (4.2) - fázové trajektórie systému (4.1) v rovine x, y.
Izoklinová metóda Na vytvorenie fázového portrétu, ktorý používajú izoklinová metóda -čiary sú nakreslené na fázovej rovine, ktoré pretínajú integrálne krivky pod jedným špecifickým uhlom. Rovnicu izokliny možno ľahko získať z (4.2). Položme Kde A–
určitú konštantnú hodnotu. Význam A predstavuje tangens uhla sklonu dotyčnice k fázovej trajektórii a môže nadobúdať hodnoty od –¥
na + ¥
. Namiesto toho nahrádzanie dy/dx v (4.2) množstvo A dostaneme izoklinovú rovnicu: .(4.3)
Rovnica (4.3) definuje v každom bode roviny jedinečnú dotyčnicu k zodpovedajúcej integrálnej krivke, s výnimkou bodu, kde P(x,y)= 0, Q (x, y) = 0
, v ktorom sa smer dotyčnice stáva neistým, pretože hodnota derivátu sa stáva neistou: Tento bod je priesečníkom všetkých izoklinál - špeciálny bod. V ňom súčasne zanikajú časové derivácie premenných X A r.
V jedinom bode sú teda miery zmeny premenných nulové. V dôsledku toho singulárny bod diferenciálnych rovníc fázových trajektórií (4.2) zodpovedá stacionárny stav systému(4.1) a jeho súradnice sú stacionárne hodnoty premenných x, y.
Zvlášť zaujímavé sú hlavné izokliny:
dy/dx=0, P(x, y)=0
–
izoklina horizontálnych dotyčníc a dy/dx=¥
, Q(x, y)=0 –
izoklina vertikálnych dotyčníc. Zostrojením hlavných izoklinál a nájdením ich priesečníka (x,y), ktorých súradnice spĺňajú podmienky:
nájdeme tak priesečník všetkých izoklín fázovej roviny, v ktorom je smer dotyčníc k fázovým trajektóriám neistý. toto - singulárny bod, čo zodpovedá stacionárny stav systému(obr. 4.2).
Systém (4.1) má toľko stacionárnych stavov, koľko je priesečníkov hlavných izoklinál na fázovej rovine. Každá fázová trajektória zodpovedá množine pohybov dynamického systému, ktoré prechádzajú rovnakými stavmi a líšia sa od seba iba na začiatku časového úseku.
, brané v kladnom smere pozdĺž kružnice L so stredom v bode z 0 ležiacom v obore analytiky funkcie f(z) (t.j. v kruhu 0<|z-z0| . (22.15.1)
a určiť ich typ.
p = 2, 3, ...)
Pozrite sa, čo je „Singulárny bod“ v iných slovníkoch:
.
|
Ak sú splnené podmienky Cauchyho vety, potom cez každý bod v priestore x, y, t existuje len jedna integrálna krivka. To isté platí, vďaka autonómii, pre fázové trajektórie: cez každý bod fázovej roviny prechádza jedna fázová trajektória.
Stabilný stav stability
Nech je systém v rovnovážnom stave.
Potom sa reprezentujúci bod nachádza v jednom zo singulárnych bodov systému, v ktorom podľa definície:
.
Či je singulárny bod stabilný alebo nie, je určené tým, či reprezentujúci bod odchádza s malou odchýlkou od stacionárneho stavu alebo nie. Vo vzťahu k sústave dvoch rovníc, definícia stability v jazykue, dnasledovne.
Rovnovážny stav je stabilný, ak pre akýkoľvek daný rozsah odchýlok od rovnovážneho stavu (e )môžete určiť oblasť d (e ), obklopujúce rovnovážny stav a majúce vlastnosť, že žiadna trajektória nezačína vo vnútri regiónu d , nikdy nedosiahne hranice e . (Obr. 4.4)
 |
|
Pre veľkú triedu systémov - hrubé systémy – charakter ktorého správania sa nemení malou zmenou tvaru rovníc, informácie o type správania v blízkosti stacionárneho stavu možno získať skúmaním nie pôvodného, ale zjednodušeného linearizované systém.
Lineárne systémy.
Zvážte systém dvoch lineárnych rovníc:
.(4.4)
Tu a B C d- konštanty, x, y- Kartézske súradnice vo fázovej rovine.
Budeme hľadať všeobecné riešenie v tvare:
.(4.5)
Dosadíme tieto výrazy do (4.4) a zredukujeme o e l t:
(4.6)
Algebraická sústava rovníc (4.6) s neznámymi A, B má nenulové riešenie iba vtedy, ak sa jeho determinant zložený z koeficientov pre neznáme rovná nule:
.
Rozšírením tohto determinantu získame charakteristickú rovnicu systému:
.(4.7)
Vyriešením tejto rovnice získate hodnoty exponentovl 1,2 , pre ktoré sú možné nenulové hodnoty A A B riešenia rovnice (4.6). Tieto významy sú
.(4.8)
Ak je radikálny výraz negatívny, potoml 1,2 komplexne konjugované čísla. Predpokladajme, že oba korene rovnice (4.7) majú nenulové reálne časti a že neexistujú žiadne viacnásobné korene. Potom je možné všeobecné riešenie sústavy (4.4) znázorniť ako lineárnu kombináciu exponenciál s exponentmil 1 , l 2 :
(4.9)
Na analýzu povahy možných trajektórií systému vo fázovej rovine používame lineárna homogénna transformácia súradníc,čo povedie systém k kanonická forma:
,(4.10)
čo umožňuje pohodlnejšie zobrazenie na fázovej rovine v porovnaní s pôvodným systémom (4.4). Zavedieme nové súradniceξ , η podľa vzorcov:
(4.1)
Z priebehu lineárnej algebry je známe, že v prípade nerovnosti na nulu sú reálne častil 1 , l 2 pôvodný systém (4.4) je možné vždy transformovať pomocou transformácií (4.11) na kanonickú formu (4.10) a študovať jeho správanie vo fázovej rovineξ , η . Pozrime sa na rôzne prípady, ktoré sa tu môžu vyskytnúť.
Korene λ 1 , λ 2 – platné a rovnakého označenia
V tomto prípade sú transformačné koeficienty reálne, pohybujeme sa z reálnej rovinyx, yk reálnej rovine ξ, η. Vydelením druhej z rovníc (4.10) prvou dostaneme:
.(4.12)
Integráciou tejto rovnice zistíme:
Kde .(4.13)
Dohodnime sa, že rozumieme λ 2 koreň charakteristickej rovnice s veľkým modulom, čo neporušuje všeobecnosť našej úvahy. Potom, keďže v posudzovanom prípade korene λ 1 , λ 2 - platné a rovnakého označenia,a>1 a máme do činenia s integrálnymi krivkami parabolického typu.
Všetky integrálne krivky (okrem osi η , čo zodpovedá ) dotknite sa začiatku osi ξ, ktorá je zároveň integrálnou krivkou rovnice (4.11). Počiatok súradníc je špeciálny bod.
Zistime teraz smer pohybu reprezentujúceho bodu pozdĺž fázových trajektórií. Ak λ 1, A2 sú teda záporné, ako je možné vidieť z rovníc (4.10), |ξ|, |η| časom klesať. Predstavujúci bod sa približuje k začiatku súradníc, ale nikdy ho nedosiahne. V opačnom prípade by to bolo v rozpore s Cauchyho vetou, ktorá hovorí, že každým bodom fázovej roviny prechádza iba jedna fázová trajektória.
Taký špeciálny bod, cez ktorý prechádzajú integrálne krivky, presne ako rodina parabol 
prechádza cez počiatok a nazýva sa uzol (obr. 4.5)
Rovnovážny stav typu uzla pri λ 1, A2 < 0 je Ljapunov stabilný, pretože reprezentujúci bod sa pohybuje pozdĺž všetkých integrálnych kriviek smerom k začiatku súradníc. Toto stabilný uzol. Ak λ 1, A2 > 0, teda |ξ|, |η| sa časom zvyšuje a reprezentujúci bod sa vzďaľuje od počiatku súradníc. V tomto prípade ide o špeciálny bod– nestabilný uzol .
Vo fázovej rovine x, y všeobecný kvalitatívny charakter správania integrálnych kriviek zostane zachovaný, ale dotyčnice k integrálnym krivkám sa nebudú zhodovať so súradnicovými osami. Uhol sklonu týchto dotyčníc bude určený pomerom koeficientov α , β , γ , δ v rovniciach (4.11).
Korene λ 1 , λ 2 – sú platné a majú rôzne znaky.
Konvertovať z súradnice x, y na súradnice ξ, η opäť skutočné. Rovnice pre kanonické premenné majú opäť tvar (4.10), ale teraz znamienka λ 1, A2 sú rôzne. Rovnica fázových trajektórií má tvar:
Kde ,(4.14)
Integrácia (4.14), nájdeme
(4.15)
Toto rovnica definuje rodinu kriviek hyperbolického typu, kde sú obe súradnicové osi- asymptoty (at a=1 mali by sme rodinu rovnostranných hyperbol). Súradnicové osi sú v tomto prípade tiež integrálne krivky– toto budú jediné integrálne krivky prechádzajúce počiatkom. Každýz ktorých pozostáva z troch fázových trajektórií: dvoch pohybov do rovnovážneho stavu (alebo z rovnovážneho stavu) a z rovnovážneho stavu. Všetky ostatné integrálne krivky– sú hyperboly, ktoré neprechádzajú počiatkom (obr. 4.6) Tento špeciálny bod sa nazýva "sedlo ». Úrovňové čiary v blízkosti horského sedla sa správajú podobne ako fázové trajektórie v blízkosti sedla.
Uvažujme o povahe pohybu reprezentujúceho bodu pozdĺž fázových trajektórií v blízkosti rovnovážneho stavu. Nech napr.λi >0, λ2<0 . Potom reprezentujúci bod umiestnený na osi ξ , sa vzdiali od počiatku a umiestni sa na os η – sa bez obmedzenia priblíži k pôvodu, bez toho, aby sme ho dosiahli v konečnom čase. Kdekoľvek je reprezentujúci bod v počiatočnom okamihu (s výnimkou singulárneho bodu a bodov na asymptote η =0), nakoniec sa vzdiali od rovnovážneho stavu, aj keď sa spočiatku pohybuje pozdĺž jednej z integrálnych kriviek smerom k singulárnemu bodu.
To je zrejmé singulárny bod, akým je sedlo, je vždy nestabilný . Len za špeciálne vybraných počiatočných podmienok na asymptoteη =0 systém sa priblíži k stavu rovnováhy. To však nie je v rozpore s tvrdením o nestabilite systému. Ak počítame, že všetky počiatočné stavy systému vo fázovej rovine sú rovnako pravdepodobné, potom pravdepodobnosť takého počiatočného stavu, ktorý zodpovedá pohybu v smere Komu singulárny bod sa rovná nule. Preto akýkoľvek skutočný pohyb odstráni systém z rovnovážneho stavu.Vráťte sa na súradnicex,y,získame rovnaký kvalitatívny obraz o charaktere pohybu trajektórií okolo počiatku súradníc.
Hranica medzi uvažovanými prípadmi uzla a sedla je prípad Kedy jedným z charakteristických ukazovateľov je napr λ 1 , zaniká, čo nastáva, keď determinant systému- výraz ad-bc=0(pozri vzorec 4.8 ). V tomto prípade sú koeficienty pravých strán rovníc (4.4) navzájom úmerné:
a systém má ako svoje rovnovážne stavy všetky body priamky:
Zostávajúce integrálne krivky sú radom rovnobežných priamok s uhlovým koeficientom , pozdĺž ktorého sa reprezentujúce body buď približujú k rovnovážnemu stavu alebo sa od neho vzďaľujú v závislosti od znamienka druhého koreňa charakteristickej rovnice λ 2 = a+d.(Obr. 4. 7 ) V tomto prípade súradnice rovnovážneho stavu závisia od počiatočnej hodnoty premenných.
Korene λ 1 , λ 2 – komplexnékonjugovať
V tomto prípade naozajX A r budeme majú komplexné konjugáty ξ , η (4.10) . Zavedením ďalšej medzitransformácie je však aj v tomto prípade možné zredukovať úvahu na skutočnú lineárnu homogénnu transformáciu. Položme:
(4.16)
Kde a,b, A u,v – skutočné hodnoty. Dá sa ukázať, že premena zx, y Komu u,v je podľa našich predpokladov reálny, lineárny, homogénny s determinantom odlišným od nuly. Na základe rovníc(4.10, 4.16) máme:
kde
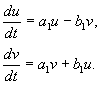(4.17)
Delenie druhej z rovníc prvou, dostaneme:
ktorý sa ľahšie integruje, ak pôjdeme do polárneho súradnicového systému (r, φ ) . Po vystriedaní dostaneme odkiaľ:
.(4.18)
Teda vo fázovej rovineu, vmáme do činenia s rodinou logaritmických špirál, z ktorých každá máasymptotický bod v počiatku.Singulárny bod, ktorý je asymptotickým bodom všetkých integrálnych kriviek, ktoré majú tvar špirál, vnorené v každomkamarát, volá sa to zameranie ( Obr.4.8 ) .
Uvažujme o povahe pohybu reprezentujúceho bodu pozdĺž fázových trajektórií. Vynásobením prvej z rovníc (4.17) číslomu, a druhý na v a pridaním dostaneme:
Kde
Nechaj a 1 < 0 (a 1 = Reλ ) . Predstavujúci bod sa potom nepretržite približuje k začiatku súradníc bez toho, aby ho dosiahol v konečnom čase. To znamená, že fázové trajektórie sú skrútené špirály a zodpovedajú tlmeným osciláciám premenné. toto - stabilné zameranie .
V prípade stabilného ohniska, rovnako ako v prípade stabilného uzla, nie je splnená len podmienka Ljapunova, ale aj prísnejšia požiadavka. Konkrétne, pre akékoľvek počiatočné odchýlky sa systém časom vráti tak blízko, ako je potrebné, k rovnovážnej polohe. Takáto stabilita, pri ktorej sa počiatočné odchýlky nielen nezvyšujú, ale klesajú s tendenciou k nule, sa nazýva absolútna stabilita .
Ak vo vzorci (4.18) a 1 >0 , potom sa reprezentujúci bod vzdiali od počiatku a máme čo do činenia s nestabilné zaostrenie . Pri presune z lietadlau,vdo fázovej rovinyX, ršpirály tiež zostanú špirálami, ale budú deformované.
Pozrime sa teraz na prípad, kedya 1
=0
. Fázové trajektórie v rovineu, vbudú kruhy 
ktoré v lietadlex, yzodpovedajú elipsám:
Teda kedy1=0 cez špeciálny bodx= 0, y= 0 neprechádza žiadna integrálna krivka. Takýto izolovaný singulárny bod, v blízkosti ktorého sú integrálne krivky uzavreté krivky, najmä elipsy vložené do seba a obklopujúce singulárny bod, sa nazýva stred.
Je teda možných šesť typov rovnovážnych stavov v závislosti od charakteru koreňov charakteristickej rovnice (4.7). Pohľad na fázové trajektórie v rovine x, y pre týchto šesť prípadov je znázornené na obr. 4.9.
Ryža. 4.9.Typy fázových portrétov v blízkosti stacionárneho stavu pre sústavu lineárnych rovníc (4.4).
Päť typov rovnovážnych stavov je drsných, ich charakter sa nemení dostatočne malými zmenami na pravej strane rovníc (4.4). V tomto prípade musia byť zmeny nielen na pravej strane, ale aj v ich derivátoch prvého rádu malé. Šiesty stav rovnováhy – stred – nie je drsný. Pri malých zmenách parametrov pravej strany rovníc sa stáva stabilným alebo nestabilným ohniskom.
Bifurkačný diagram
Predstavme si nasledujúci zápis:
.
(4.11)
Potom bude charakteristická rovnica napísaná ako:
.
(4.12)
Uvažujme rovinu s pravouhlými karteziánskymi súradnicami s , D a vyznačte na ňom oblasti zodpovedajúce jednému alebo druhému typu rovnovážneho stavu, ktorý je určený povahou koreňov charakteristickej rovnice
.(4.13)
Podmienkou stability rovnovážneho stavu bude prítomnosť negatívnej reálnej časti yl 1 a l 2 . Nevyhnutnou a postačujúcou podmienkou na to je splnenie nerovnostís > 0, D > 0 . V diagrame (4.15) táto podmienka zodpovedá bodom umiestneným v prvej štvrtine roviny parametrov. Singulárny bod bude ohniskom, akl 1 a l 2 komplexné. Táto podmienka zodpovedá tým bodom roviny, pre ktoré , tie. body medzi dvoma vetvami parabolys 2 = 4 D. Body nápravy s = 0, D>0, zodpovedajú rovnovážnym stavom stredového typu. podobne,l 1 a l 2 - sú platné, ale rôznych znakov, t.j. singulárny bod bude sedlom ak D<0, atď. V dôsledku toho dostaneme diagram rozdelenia roviny parametrov s, D, do oblastí zodpovedajúcich rôznym typom rovnovážnych stavov.
Ryža. 4.10. Bifurkačný diagram
pre sústavu lineárnych rovníc 4.4
Ak sú koeficienty lineárneho systému a B C d závisí od určitého parametra, potom keď sa tento parameter zmení, zmenia sa aj hodnotys , D . Pri prekračovaní hraníc sa kvalitatívne mení charakter fázového portrétu. Preto sa takéto hranice nazývajú bifurkačné hranice – na opačných stranách hranice má systém dva topologicky odlišné fázové portréty a podľa toho aj dva rôzne typy správania.
Diagram ukazuje, ako k takýmto zmenám môže dôjsť. Ak vylúčime špeciálne prípady - pôvod súradníc - potom je ľahké vidieť, že sedlo sa môže pri prekročení ordinátnej osi premeniť na uzol, stabilný alebo nestabilný. Stabilný uzol môže ísť buď do sedla alebo do stabilného ohniska atď. Všimnite si, že prechody stabilný uzol - stabilné ohnisko a nestabilný uzol - nestabilné ohnisko nie sú bifurkácie, pretože topológia fázového priestoru sa nemení. Viac o topológii fázového priestoru a bifurkačných prechodoch si povieme v 6. prednáške.
Pri bifurkačných prechodoch sa mení charakter stability singulárneho bodu. Napríklad stabilné zaostrenie cez stred sa môže zmeniť na nestabilné zaostrenie. Táto bifurkácia sa nazýva Andronov-Hopfova bifurkácia podľa mien vedcov, ktorí to skúmali. Počas tejto bifurkácie v nelineárnych systémoch sa rodí limitný cyklus a systém sa stáva samooscilujúcim (pozri prednášku 8).
Príklad. Systém lineárnej chemickej reakcie
Látka X prúdi zvonku konštantnou rýchlosťou, mení sa na látku Y a rýchlosťou úmernou koncentrácii látky Y, je odstránený zo sféry reakcie. Všetky reakcie sú prvého rádu, s výnimkou prílevu látky zvonku, ktorý je nultého rádu. Reakčná schéma vyzerá takto:
(4.14)
a je opísaná sústavou rovníc:
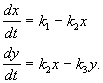(4.15)
Stacionárne koncentrácie získame porovnaním pravej strany s nulou:
.(4.16)
Zoberme si fázový portrét systému. Vydeľme druhú rovnicu sústavy (4.16) prvou. Dostaneme:
.(4.17)
Rovnica (4.17) určuje správanie premenných vo fázovej rovine. Vytvorme fázový portrét tohto systému. Najprv nakreslíme hlavné izokliny na fázovej rovine. Rovnica izokliny vertikálnych dotyčníc:
Rovnica izokliny horizontálnych dotyčníc:
Singulárny bod (stacionárny stav) leží na priesečníku hlavných izoklinál.
Teraz určme, pod akým uhlom sa súradnicové osi pretínajú s integrálnymi krivkami.
Ak x= 0, potom .
Teda dotyčnica dotyčnice k integrálnym krivkám y=y(x), pretínajúca súradnicovú os x=0, je záporná v hornej polrovine (nezabudnite, že premenné x, y majú hodnoty koncentrácie, a preto nás zaujíma iba pravý horný kvadrant fázovej roviny). V tomto prípade sa dotyčnica uhla dotyčnice zvyšuje so vzdialenosťou od počiatku.
Zvážte os y= 0. V bode, kde táto os pretína integrálne krivky, sú opísané rovnicou
o dotyčnica sklonu integrálnych kriviek pretínajúcich os úsečky je kladná a zvyšuje sa od nuly do nekonečna so zvyšujúcou sa X.
o .
Potom s ďalším zvyšovaním tangens uhla sklonu klesá v absolútnej hodnote, zostáva záporná a má tendenciu k -1 pri X ® ¥ . Keď poznáme smer dotyčníc k integrálnym krivkám na hlavných izoklinách a na súradnicových osiach, je ľahké zostaviť celý obraz fázových trajektórií.
 |
|
Stanovme povahu stability singulárneho bodu pomocou Ljapunovovej metódy. Charakteristický determinant systému má tvar:
.
Rozšírením determinantu získame charakteristickú rovnicu systému: , t.j. Korene charakteristickej rovnice sú oba záporné. V dôsledku toho je stacionárny stav systému stabilným uzlom. V tomto prípade koncentrácia látky X smeruje k stacionárnemu stavu vždy monotónne, koncentrácia látky Y môže prechádzať min alebo max. Oscilačné režimy sú v takomto systéme nemožné.
