Racionální funkce je zlomek tvaru , jehož čitatel a jmenovatel jsou polynomy nebo součiny polynomů.
Příklad 1 Krok 2.
.
Neurčené koeficienty vynásobíme polynomy, které nejsou v tomto jednotlivém zlomku, ale které jsou v jiných výsledných zlomcích:
Otevřeme závorky a přirovnáme čitatele původního integrandu k výslednému výrazu:
Na obou stranách rovnosti hledáme členy se stejnými mocninami x a skládáme z nich soustavu rovnic:
.
Zrušíme všechna x a získáme ekvivalentní systém rovnic:
.
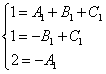Konečná expanze integrandu na součet jednoduchých zlomků je tedy:
.
Příklad 2 Krok 2. V kroku 1 jsme získali následující rozklad původního zlomku na součet jednoduchých zlomků s neurčenými koeficienty v čitatelích:
.
Nyní začneme hledat nejisté koeficienty. Abychom to udělali, přirovnáme čitatele původního zlomku ve funkčním výrazu k čitateli výrazu získaného po zmenšení součtu zlomků na společného jmenovatele:
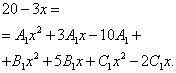
Nyní je potřeba vytvořit a vyřešit soustavu rovnic. K tomu srovnáme koeficienty proměnné na odpovídající stupeň v čitateli původního výrazu funkce a podobné koeficienty ve výrazu získaném v předchozím kroku:
Vyřešíme výsledný systém:
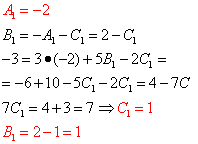
Takže odtud
.
Příklad 3 Krok 2. V kroku 1 jsme získali následující rozklad původního zlomku na součet jednoduchých zlomků s neurčenými koeficienty v čitatelích:
Začneme hledat nejisté koeficienty. Abychom to udělali, přirovnáme čitatele původního zlomku ve funkčním výrazu k čitateli výrazu získaného po zmenšení součtu zlomků na společného jmenovatele:
Stejně jako v předchozích příkladech sestavíme soustavu rovnic:
Zmenšíme x a dostaneme ekvivalentní systém rovnic:
Řešením systému získáme následující hodnoty nejistých koeficientů:
Získáme konečný rozklad integrandu na součet jednoduchých zlomků:
.
Příklad 4. Krok 2. V kroku 1 jsme získali následující rozklad původního zlomku na součet jednoduchých zlomků s neurčenými koeficienty v čitatelích:
.
Z předchozích příkladů již víme, jak dát čitatel původního zlomku na roveň výrazu v čitateli získaném po rozložení zlomku na součet jednoduchých zlomků a přivedení tohoto součtu na společného jmenovatele. Proto pouze pro účely kontroly uvádíme výsledný systém rovnic:
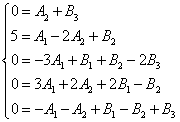
Řešením systému získáme následující hodnoty nejistých koeficientů:
Získáme konečný rozklad integrandu na součet jednoduchých zlomků:
Příklad 5. Krok 2. V kroku 1 jsme získali následující rozklad původního zlomku na součet jednoduchých zlomků s neurčenými koeficienty v čitatelích:
.
Tento součet nezávisle zredukujeme na společného jmenovatele, čímž přirovnáme čitatele tohoto výrazu k čitateli původního zlomku. Výsledkem by měl být následující systém rovnic:
Řešením systému získáme následující hodnoty nejistých koeficientů:
.
Získáme konečný rozklad integrandu na součet jednoduchých zlomků:
.
Příklad 6. Krok 2. V kroku 1 jsme získali následující rozklad původního zlomku na součet jednoduchých zlomků s neurčenými koeficienty v čitatelích:
S tímto množstvím provedeme stejné akce jako v předchozích příkladech. Výsledkem by měl být následující systém rovnic:
Řešením systému získáme následující hodnoty nejistých koeficientů:
.
Získáme konečný rozklad integrandu na součet jednoduchých zlomků:
.
Příklad 7. Krok 2. V kroku 1 jsme získali následující rozklad původního zlomku na součet jednoduchých zlomků s neurčenými koeficienty v čitatelích:
.
Po určitých akcích s výsledným množstvím by měl být získán následující systém rovnic:
Řešením systému získáme následující hodnoty nejistých koeficientů:
Získáme konečný rozklad integrandu na součet jednoduchých zlomků:
.
Příklad 8. Krok 2. V kroku 1 jsme získali následující rozklad původního zlomku na součet jednoduchých zlomků s neurčenými koeficienty v čitatelích:
.
Udělejme nějaké změny v akcích, které již byly převedeny do automatizace, abychom získali systém rovnic. Existuje umělá technika, která v některých případech pomáhá vyhnout se zbytečným výpočtům. Přivedením součtu zlomků ke společnému jmenovateli získáme a přirovnáním čitatele tohoto výrazu k čitateli původního zlomku získáme.
Zde poskytujeme podrobná řešení tří příkladů integrace následujících racionálních zlomků:
,
,
.
Příklad 1
Vypočítejte integrál:
.
Řešení
Zde je pod znaménkem integrálu racionální funkce, protože integrand je zlomkem polynomů. Stupeň polynomu jmenovatele ( 3 ) je menší než stupeň polynomu čitatele ( 4 ). Nejprve je tedy potřeba vybrat celou část zlomku.
1.
Vyberme celou část zlomku. Rozdělit x 4
podle x 3 - 6 x 2 + 11 x - 6:
Odtud
.
2.
Rozložme jmenovatele zlomku na faktor. Chcete-li to provést, musíte vyřešit kubickou rovnici:
.
6
1, 2, 3, 6, -1, -2, -3, -6
.
Dosadíme x = 1
:
.
1
. Dělit x - 1
:
Odtud
.
Řešení kvadratické rovnice.
.
Kořeny rovnice jsou: , .
Pak
.
3.
Rozeberme zlomek do jeho nejjednodušší podoby.
.
Tak jsme našli:
.
Pojďme se integrovat.
Odpovědět
Příklad 2
Vypočítejte integrál:
.
Řešení
Zde je čitatelem zlomku polynom nultého stupně ( 1 = x 0). Jmenovatel je polynom třetího stupně. Protože 0 < 3 , pak je zlomek správný. Pojďme si to rozdělit na jednoduché zlomky.
1.
Rozložme jmenovatele zlomku na faktor. Chcete-li to provést, musíte vyřešit rovnici třetího stupně:
.
Předpokládejme, že má alespoň jeden celý kořen. Pak je to dělitel čísla 3
(člen bez x). To znamená, že celý kořen může být jedno z čísel:
1, 3, -1, -3
.
Dosadíme x = 1
:
.
Našli jsme tedy jeden kořen x = 1
. Rozdělit x 3 + 2 x - 3 na x- 1
:
Tak,
.
Řešení kvadratické rovnice:
X 2 + x + 3 = 0.
Najděte diskriminant: D = 1 2 - 4 3 = -11. Protože D< 0
, pak rovnice nemá žádné skutečné kořeny. Tak jsme získali faktorizaci jmenovatele:
.
2.
.
(x - 1) (x 2 + x + 3):
(2.1)
.
Dosadíme x = 1
. Pak x- 1 = 0
,
.
Pojďme se nahradit (2.1)
x = 0
:
1 = 3 A - C;
.
Srovnejme se (2.1)
koeficienty pro x 2
:
;
0 = A + B;
.
.
3.
Pojďme se integrovat.
(2.2)
.
Pro výpočet druhého integrálu izolujeme derivaci jmenovatele v čitateli a redukujeme jmenovatele na součet druhých mocnin.
;
;
.
Vypočítejte I 2
.
.
Protože rovnice x 2 + x + 3 = 0 nemá žádné skutečné kořeny, pak x 2 + x + 3 > 0. Proto lze znaménko modulu vynechat.
Dodáváme do (2.2)
:
.
Odpovědět
Příklad 3
Vypočítejte integrál:
.
Řešení
Zde pod znaménkem integrálu je zlomek polynomů. Proto je integrand racionální funkcí. Stupeň polynomu v čitateli je roven 3 . Stupeň polynomu jmenovatele zlomku je roven 4 . Protože 3 < 4 , pak je zlomek správný. Proto se dá rozložit na jednoduché zlomky. Ale k tomu musíte faktorizovat jmenovatele.
1.
Rozložme jmenovatele zlomku na faktor. Chcete-li to provést, musíte vyřešit rovnici čtvrtého stupně:
.
Předpokládejme, že má alespoň jeden celý kořen. Pak je to dělitel čísla 2
(člen bez x). To znamená, že celý kořen může být jedno z čísel:
1, 2, -1, -2
.
Dosadíme x = -1
:
.
Našli jsme tedy jeden kořen x = -1
. Dělit x - (-1) = x + 1:
Tak,
.
Nyní musíme vyřešit rovnici třetího stupně:
.
Pokud předpokládáme, že tato rovnice má celočíselný kořen, pak je to dělitel čísla 2
(člen bez x). To znamená, že celý kořen může být jedno z čísel:
1, 2, -1, -2
.
Dosadíme x = -1
:
.
Takže jsme našli další kořen x = -1
. Bylo by možné, stejně jako v předchozím případě, rozdělit polynom , ale seskupíme členy:
.
Protože rovnice x 2 + 2 = 0
nemá žádné skutečné kořeny, pak dostaneme faktorizaci jmenovatele:
.
2.
Rozeberme zlomek do jeho nejjednodušší podoby. Hledáme rozšíření ve formě:
.
Zbavíme se jmenovatele zlomku, vynásobíme (x + 1) 2 (x 2 + 2):
(3.1)
.
Dosadíme x = -1
. Potom x + 1 = 0
,
.
Pojďme rozlišovat (3.1)
:
;
.
Dosadíme x = -1
a vzít v úvahu, že x + 1 = 0
:
;
;
.
Pojďme se nahradit (3.1)
x = 0
:
0 = 2 A + 2 B + D;
.
Srovnejme se (3.1)
koeficienty pro x 3
:
;
1 = B + C;
.
Našli jsme tedy rozklad na jednoduché zlomky:
.
3.
Pojďme se integrovat.
.
2.,
5.
,
3.
,
6.
.
V integrálech 1-3 jako u
akceptovat 
. Takže potom n-násobnou aplikací vzorce (19) dojdeme k jednomu z tabulkových integrálů
,
,
.
V integrálech 4-6 při derivování zjednodušte transcendentální faktor 
,
nebo 
, což je třeba brát jako u.
Vypočítejte následující integrály.
Příklad 7.
Příklad 8. 
Redukce integrálů na sebe
Pokud integrand 
má tvar:
,
,
a tak dále,
pak po dvojitém integrování po částech získáme výraz obsahující původní integrál 
:
,
Kde 
- nějaké konstantní.
Řešení výsledné rovnice pro 
, získáme vzorec pro výpočet původního integrálu:
.
Tento případ aplikace metody integrace po částech se nazývá " přivedení integrálu k sobě samému».
Příklad 9. Vypočítejte integrál
.
Na pravé straně je původní integrál 
. Přesunutím na levou stranu dostaneme:
.
Příklad 10. Vypočítejte integrál
.
4.5. Integrace nejjednodušších vlastních racionálních zlomků
Definice.Nejjednodušší vlastní zlomky já , II A III typy Nazývají se následující zlomky:
já.
;
II.
;
(
- kladné celé číslo);
III.
; (kořeny jmenovatele jsou složité, to znamená: 
.
Uvažujme integrály jednoduchých zlomků.
já.
;
(20)
II. ; (21)
III.
;
Čitatele zlomku transformujeme tak, abychom izolovali člen v čitateli 
, rovnající se derivaci jmenovatele.
Uvažujme první ze dvou získaných integrálů a proveďte v něm změnu:
Ve druhém integrálu přidáme jmenovatele k dokonalému čtverci:
A konečně, integrál zlomku třetího typu se rovná:
=
+
.
(22)
Integrál nejjednodušších zlomků typu I je tedy vyjádřen logaritmy, typ II - racionálními funkcemi, typ III - logaritmy a arktangens.
4.6.Integrace zlomkově-racionálních funkcí
Jednou z tříd funkcí, které mají integrál vyjádřený pomocí elementárních funkcí, je třída algebraických racionálních funkcí, tedy funkcí vyplývajících z konečného počtu algebraických operací s argumentem.
Každá racionální funkce 
lze vyjádřit jako podíl dvou polynomů 
A 
:
.
(23)
Budeme předpokládat, že polynomy nemají společné kořeny.
Zavolá se zlomek formuláře (23). opravit, je-li stupeň čitatele menší než stupeň jmenovatele, tzn. m< n. V opačném případě - špatně.
Je-li zlomek nevlastní, pak dělením čitatele jmenovatelem (podle pravidla pro dělení mnohočlenů) uvedeme zlomek jako součet mnohočlenu a vlastního zlomku:
,
(24)
Kde 
- polynom, 
- vlastní zlomek a stupeň polynomu 
- ne vyšší než stupeň ( n-1).
Příklad. 
Protože integrace polynomu je redukována na součet tabelovaných integrálů mocninné funkce, hlavní potíž při integraci racionálních zlomků spočívá v integraci správných racionálních zlomků.
V algebře bylo dokázáno, že každý správný zlomek 
se rozloží na součet výše uvedeného prvoci zlomky, jejichž tvar je určen kořeny jmenovatele 
.
Uvažujme tři speciální případy. Zde a dále budeme předpokládat, že koeficient 
na nejvyšším stupni jmenovatele 
rovný jedné 
=1, tznredukovaný polynom
.
Případ 1 Kořeny jmenovatele, tedy kořeny 
rovnic 
=0, jsou platné a odlišné. Potom představujeme jmenovatele jako součin lineárních faktorů:
a správný zlomek se rozloží na nejjednodušší zlomky I-gotypu:
,
(26)
Kde 
– některá konstantní čísla, která se nalézají metodou neurčitých koeficientů.
K tomu potřebujete:
1. Přiveďte pravou stranu expanze (26) ke společnému jmenovateli.
2. Srovnejte koeficienty shodných mocnin shodných polynomů v čitateli levé a pravé strany. Získáme soustavu lineárních rovnic k určení 
.
3. Vyřešte výslednou soustavu a najděte neurčené koeficienty 
.
Potom se integrál zlomkově-racionální funkce (26) bude rovnat součtu integrálů nejjednodušších zlomků typu I, vypočítaného podle vzorce (20).
Příklad. Vypočítejte integrál 
.
Řešení. Rozložme jmenovatele na faktor pomocí Vietovy věty:
Poté se integrandová funkce rozloží na součet jednoduchých zlomků:
.
X:
Napišme soustavu tří rovnic, abychom našli 
X na levé a pravé straně:
.
Naznačme jednodušší způsob hledání nejistých koeficientů, tzv metoda částečné hodnoty.
Za předpokladu rovnosti (27) 
dostaneme 
, kde 
. Věřící 
dostaneme 
. Konečně věřit 
dostaneme 
.
.
Případ 2 Kořen jmenovatele 
jsou platné, ale mezi nimi je více (stejných) kořenů. Potom jmenovatele reprezentujeme jako součin lineárních faktorů zahrnutých v součinu do té míry, že násobnost odpovídajícího kořene je:
Kde 
.
Správný zlomek 
součet zlomků typu I a II bude rozložen. Ať např. 
- kořen jmenovatele násobnosti k a všichni ostatní ( n-
k) kořeny jsou různé.
Poté bude rozšíření vypadat takto:
Stejně tak, pokud existují další vícenásobné kořeny. Pro nenásobné kořeny zahrnuje expanze (28) nejjednodušší zlomky prvního typu.
Příklad. Vypočítejte integrál 
.
Řešení. Představme si zlomek jako součet nejjednodušších zlomků prvního a druhého druhu s neurčitými koeficienty:
.
Přivedeme pravou stranu ke společnému jmenovateli a přirovnáme polynomy v čitatelích levé a pravé strany:
Na pravé straně uvádíme podobné se stejnými stupni X:
Napišme soustavu čtyř rovnic, abychom našli 
A 
. K tomu srovnáme koeficienty se stejnými mocninami X na levé a pravé straně
.
Případ 3 Mezi kořeny jmenovatele 
existují složité jednotlivé kořeny. To znamená, že rozšíření jmenovatele zahrnuje faktory druhého stupně 
, nerozložitelné na reálné lineární faktory a neopakují se.
Potom při rozkladu zlomku bude každý takový faktor odpovídat nejjednoduššímu zlomku typu III. Lineární faktory odpovídají nejjednodušším zlomkům typů I a II.
Příklad. Vypočítejte integrál 
.
Řešení.
.
.
.
Dříve jsme diskutovali o obecných metodách integrace. V tomto a následujících odstavcích budeme hovořit o integraci konkrétních tříd funkcí pomocí diskutovaných technik.
Integrace nejjednodušších racionálních funkcí
Uvažujme integrál formuláře \textstyle(\int R(x)\,dx), kde y=R(x) je racionální funkce. Jakýkoli racionální výraz R(x) může být reprezentován ve tvaru \frac(P(x))(Q(x)), kde P(x) a Q(x) jsou polynomy. Je-li tento zlomek nevlastní, to znamená, je-li stupeň v čitateli větší nebo roven stupni jmenovatele, lze jej reprezentovat jako součet polynomu (celočíselné části) a vlastního zlomku. Proto stačí uvažovat o integraci vlastních zlomků.
Ukažme, že integrace takových zlomků se redukuje na integraci jednoduché zlomky, tedy výrazy ve tvaru:
\mathsf(1))~\frac(A)(x-a);\quad \mathsf(2))~\frac(A)((x-a)^n);\quad \mathsf(3))~ \frac( Ax+B)(x^2+px+q);\quad \mathsf(4))~\frac(Ax+B)((x^2+px+q)^n).
Kde A,\,B,\,a,\,p,\,q jsou reálná čísla a čtvercová trojčlenka x^2+px+q nemá žádné reálné kořeny. Výrazy typu 1) a 2) se nazývají zlomky 1. druhu a výrazy typu 3) a 4) zlomky 2. druhu.
Integrály zlomků 1. druhu se počítají přímo
\begin(zarovnáno)\mathsf(1))&~\int\frac(A)(x-a)\,dx= A\ln|x-a|+C;\\ \mathsf(2))&~ \int\frac (A)((x-a)^n)\,dx= A\int(x-a)^(-n)\,dx= A\,\frac((x-a)^(-n+1))(-n+ 1 )+C~(n=2,3,4,\ldots). \end (zarovnáno)
Uvažujme výpočet integrálů zlomků 2. druhu: \mathsf(3))~ \int\frac(Ax+B)(x^2+px+q)\,dx\,.
Nejprve si toho všimneme
\int\frac(dt)(t^2+a^2)= \frac(1)(a)\jméno operátora (arctg)\frac(t)(a)+C,\qquad \int\frac(t\ ,dt)(t^2+a^2)= \frac(1)(2)\ln(t^2+a^2)+C.
Abychom zredukovali výpočet integrálu 3) na tyto dva integrály, transformujeme čtvercový trinom x^2+px+q tak, že z něj oddělíme celý čtverec:
x^2+px+q= (\left(x+\frac(p)(2)\right)\^2+ \left(q-\frac{p^2}{4}\right)\!. !}
Protože podle předpokladu tento trinom nemá žádné skutečné kořeny q-\frac(p^2)(4)>0 a můžeme dát q-\frac(p^2)(4)=a^2. Náhrada x+\frac(p)(2)=t,~ dx=dt transformuje integrál 3) na lineární kombinaci uvedených dvou integrálů:
\begin(zarovnáno)\int\frac(Ax+B)(x^2+px+q)\,dx&= \int\frac(A\!\left(t-\frac(p)(2)\vpravo )+B)(t^2+a^2)\,dt= A\int\frac(t\,dt)(t^2+a^2)+ \left(B-\frac(Ap)(2 )\right)\!\int\frac(dt)(t^2+a^2)=\\ &=\frac(A)(2)\ln(t^2+a^2)+ \frac( 1)(a)\!\left(B-\frac(Ap)(2)\vpravo)\!\ \operatorname(arctg)\frac(t)(a)+C. \end (zarovnáno)
V konečné odpovědi stačí nahradit (t) x+\frac(p)(2) a (a) za \sqrt(q-\frac(p^2)(4)). Protože t^2+a^2=x^2+px+q, tak
\int\frac(Ax+B)(x^2+px+q)\,dx= \frac(A)(2)\ln(x^2+px+q)+ \frac(B-\dfrac( Ap)(2))(\sqrt(q-\dfrac(p^2)(4))) \název operátora(arctg)\frac(x+\dfrac(p)(2))(\sqrt(q-\dfrac (p^2)(4)))+C.
Zvažte případ \mathsf(4))~ \int\frac(Ax+B)((x^2+px+q)^n)\,dx.
Stejně jako v předchozím případě nastavme x+\frac(p)(2)=t. Dostaneme:
\int\frac(Ax+B)((x^2+px+q)^n)\,dx= A\int\frac(t\,dt)((t^2+a^2)^n) + \left(B-\frac(Ap)(2)\vpravo)\! \int\frac(dt)((t^2+a^2)^n)\,.
První termín se vypočítá takto:
A\int\frac(t\,dt)((t^2+a^2)^n)= \frac(A)(2)\int(t^2+a^2)^(-n)\ ,d(t^2+a^2)= \frac(A)(2)\frac((t^2+a^2)^(-n+1))(-n+1)= \frac( A)(2(1-n)(t^2+a^2)^(n-1))\,.
Druhý integrál se vypočítá pomocí vzorce pro opakování.
Příklad 1 Pojďme počítat \int\frac(3x+2)(x^2+2x+3)\,dx.
Řešení. My máme: x^2+2x+3=(x+1)^2+2. Dejme x+1=t. Potom dx=dt a 3x+2=3(t-1)+2=3t-1 a proto
\begin(zarovnáno)\int\frac(3x+2)(x^2+2x+3)\,dx&= \int\frac(3t-1)(t^2+2)\,dt= \frac( 3)(2)\int\frac(2t\,dt)(t^2+2)- \int\frac(dt)(t^2+(\sqrt(2))^2)=\\ &= \frac(3)(2)\ln(t^2+2)- \frac(1)(\sqrt(2))\název operátora(arctg)\frac(t)(\sqrt(2))+C= \\ &=\frac(3)(2)\ln(x^2+2x+3)- \frac(1)(\sqrt(2))\název operátora(arctg)\frac(x+1)(\ sqrt(2))+C. \end (zarovnáno)
Příklad 2 Pojďme počítat \int\frac(x+2)((x^2+6x+10)^2)\,dx.
Řešení. My máme: x^2+6x+10=(x+3)^2+1. Zavedeme novou proměnnou nastavením x+3=t. Potom dt=dx a x+2=t-1. Nahrazením proměnné pod znaménkem integrálu získáme:
\begin(zarovnáno)\int\frac(x+2)((x^2+6x+10)^2)\,dx&= \int\frac(t-1)((t^2+1)^2 )\,dt= \frac(1)(2)\int\frac(2t\,dt)((t^2+1)^2)-\int\frac(dt)((t^2+1) ^2)=\\ &=-\frac(1)(2(t^2+1))- \int\frac(dt)((t^2+1)^2)\,. \end(zarovnáno))
Položme I_2=\int\frac(dt)((t^2+1)^2). My máme:
I_2=\frac(1)(2)I_1+\frac(1)(2)\frac(t)(t^2+1), Ale I_1=\int\frac(dt)(t^2+1)= \operatorname(arctg)t Tím pádem, I_2= \frac(1)(2)\jméno operátora(arctg)t+ \frac(t)(2(t^2+1)).
Nakonec dostaneme:
\begin(zarovnáno)\int\frac(x+2)((x^2+6x+10)^2)\,dx&=-\frac(1)(2(t^2+1))-\frac (1)(2)\jméno operátora(arctg)t-\frac(t)(2(t^2+1))=\\ &=-\frac(1)(2(x^2+6x+10) )- \frac(1)(2)\operatorname(arctg)(x+3)- \frac(x+3)(2(x^2+6x+10))+C=\\ &=\frac( -x-4)(2(x^2+6x+10))-\frac(1)(2)\jméno operátora(arctg)(x+3)+C \end(zarovnáno)
Integrace správných zlomků
Zvažte správný zlomek R(x)=\frac(P(x))(Q(x)), kde Q(x) je polynom stupně n. Bez ztráty obecnosti můžeme předpokládat, že vedoucí koeficient v Q(x) je roven 1. V kurzu algebry je prokázáno, že takový polynom s reálnými koeficienty lze faktorizovat na faktory prvního a druhého stupně s reálnými koeficienty :
Q(x)= (x-x_1)^(\alpha)\ldots (x-x_k)^(\beta) (x^2+p\,x+q)^(\gamma)\ldots (x^2 +r\,x+s)^(\delta).
kde x_1,\ldots,x_k jsou skutečné kořeny polynomu Q(x) a čtvercové trinomy nemají žádné skutečné kořeny. Lze dokázat, že pak R(x) je reprezentováno jako součet jednoduchých zlomků tvaru 1) -4):
\begin(zarovnáno)R(x)=&\frac(P(x))(Q(x))= \frac(A_1)((x-x_1)^(\alpha))+ \frac(A_2)( (x-x_1)^(\alpha-1))+\ldots+ \frac(A_(\alpha))(x-x_1)\,+\\ &+\,\ldots+ \frac(B_1)((x- x_k)^(\beta))+ \frac(B_2)((x-x_k)^(\beta-1))+\ldots+ \frac(B_(\beta))(x-x_k)+ \frac(M_1x+ N_1)((x^2+p\,x+q)^(\gamma))\,+\\ &+\,\ldots+ \frac(M_(\gamma)+ N_(\gamma))(x^ 2+ p\,x+s)+ \frac(E_1x+F_1)((x^2+rx+s)^(\delta))+\ldots+ \frac(E_(\delta)x+F_(\delta ))(x^2+rx+s)\, \end(zarovnáno)
kde exponenty jmenovatelů postupně klesají z \alpha na 1, ..., z \beta do 1, z \gamma na 1, ..., z \delta do 1, a A_1,\ldots,F_(\delta)- nejisté koeficienty. Abychom našli tyto koeficienty, je nutné se zbavit jmenovatelů a po získání rovnosti dvou polynomů použít metodu neurčitých koeficientů.
Další způsob, jak určit kurzy A_1,\ldots, A_(\alpha), \ldots, F_(\delta) je založeno na substituci hodnot proměnné x. Dosazením libovolného čísla místo x do rovnosti získané z rovnosti (1) po odstranění jmenovatelů dojdeme k lineární rovnici pro požadované koeficienty. Dosazením potřebného počtu takovýchto dílčích hodnot proměnné získáme soustavu rovnic pro nalezení koeficientů. Nejvýhodnější je zvolit kořeny jmenovatele (reálné i komplexní) jako soukromé hodnoty proměnné. V tomto případě téměř všechny členy na pravé straně rovnosti (to znamená rovnost dvou polynomů) zmizí, což usnadňuje nalezení zbývajících koeficientů. Při dosazování komplexních hodnot mějte na paměti, že dvě komplexní čísla jsou si rovna právě tehdy, když se jejich skutečná a imaginární část rovnají. Z každé rovnosti obsahující komplexní čísla jsou tedy získány dvě rovnice.
Po nalezení neurčených koeficientů zbývá vypočítat integrály nejjednodušších získaných zlomků. Protože při integraci nejjednodušších zlomků, jak jsme viděli, se získají pouze racionální funkce, arkustangens a logaritmy, pak integrál jakékoli racionální funkce je vyjádřen prostřednictvím racionální funkce, arctangens a logaritmy.
Příklad 3 Vypočítejme integrál vlastního racionálního zlomku \int\frac(6x+1)(x^2+2x-3)\,dx.
Řešení. Rozložme jmenovatele integrandu na faktor:
x^2+2x-3=(x-1)(x+3).
Zapišme si integrand a prezentujme jej jako součet jednoduchých zlomků:
\frac(6x+1)(x^2+2x-3)= \frac(A)(x-1)+\frac(B)(B+3)\,.
Když se osvobodíme od jmenovatelů v této rovnosti, dostaneme:
6x+1=A\cdot (x+3)+B\cdot (x-1)\,.
Pro zjištění koeficientů použijeme metodu substituce dílčích hodnot. Abychom našli koeficient A, nastavme x=1. Pak z rovnosti (2) dostaneme 7=4A, odkud A=7/4. Abychom našli koeficient B, nastavme x=-3. Pak z rovnosti (2) dostaneme -17=-4B, odkud B=17/4.
Tak, \frac(6x+1)(x^2+2x-3)= \frac(7)(4)\cdot\frac(1)(x-1)+ \frac(17)(4)\cdot\frac (1) (x+3). Prostředek,
\int\frac(6x+1)(x^2+2x-3)\,dx= \frac(7)(4)\int\frac(dx)(x-1)+ \frac(17)(4 )\int\frac(dx)(x+3)= \frac(7)(4)\ln|x-1|+ \frac(17)(4)\ln|x+3|+C.
Příklad 4. Pojďme počítat \int\frac(x^4+2x^2+8x+5)((x^2+2)(x-1)^2(x+2))\,dx.
Řešení. Vypišme integrand a prezentujme jej jako součet jednoduchých zlomků. Jmenovatel obsahuje faktor x^2+2, který nemá skutečné kořeny, odpovídá zlomku 2. druhu: \frac(Ax+B)(x^2+2) násobitel (x-1)^2 odpovídá součtu dvou zlomků 1. druhu: \frac(C)((x-1)^2)+ \frac(D)(x-1); konečně faktor x+2 odpovídá jednomu zlomku 1. druhu \frac(E)(x+2) . Integrandovou funkci tedy reprezentujeme jako součet čtyř zlomků:
\frac(x^4+2x^2+8x+5)((x^2+2)(x-1)^2(x+2))= \frac(Ax+B)(x^2+2 )+ \frac(C)((x-1)^2)+ \frac(D)(x-1)+ \frac(E)(x+2)\,.
Osvoboďme se od jmenovatelů v této rovnosti. Dostaneme:
\begin(zarovnáno) x^4+2x^2+8x+5&= (Ax+B)(x-1)^2(x+2)+ C(x^2+2)(x+2)\, +\\ &\phantom(=)+ D(x^2+2)(x-1)(x+2)+ E(x^2+2)(x-1)^2.\end(zarovnáno)
Jmenovatel integrandu má dva reálné kořeny: x=1 a x=-2. Při dosazení hodnoty x=1 do rovnosti (4) dostaneme 16=9C, ze kterého zjistíme C=16/9. Při dosazení x=-2 dostaneme 13=54E a podle toho definujeme E=13/54. Dosazením hodnoty x=i\,\sqrt(2) (kořen polynomu x^2+2 ) můžeme přejít k rovnosti
4-4+8\,i\,\sqrt(2)+5= (A\,i\,\sqrt(2)+B)\cdot (i\,\sqrt(2)-1)^2\ cdot (i\,\sqrt(2)+2).
Transformuje se do tvaru:
(10A+2B)+(2A-5B)\sqrt(2)\,i= 5+8\sqrt(2)\,i, odkud 10A+2B=5, a (2A-5B)\sqrt(2)=8\sqrt(2).
Řešení soustavy dvou rovnic se dvěma proměnnými \begin(cases)10A+2B=5,\\ 2A-5B=8,\end(cases) shledáváme: A=\frac(41)(54),~ B=-\frac(35)(27).
Zbývá určit hodnotu koeficientu D. Chcete-li to provést, otevřeme závorky v rovnosti (4), uvedeme podobné pojmy a pak porovnáme koeficienty pro x^4. Dostaneme:
A+D+E=1, tedy D=0.
Nalezené hodnoty koeficientů dosadíme do rovnosti (3):
\frac(x^4+2x^2+8x+5)((x^2+2)(x-1)^2(x+2))= \frac(\drac(41)(54)\, x- \dfrac(35)(27))(x^2+2)+ \frac(16)(9)\frac(1)((x-1)^2)+ \frac(13)(54) \frac(1)(x+2)\,
a poté přejděte k integraci:
\begin(zarovnáno)\int\frac(x^4+2x^2+8x+5)((x^2+2)(x-1)^2(x+2))\,dx&= \frac( 41)(54)\int\frac(x\,dx)(x^2+2)- \frac(35)(27)\int\frac(dx)(x^2+2)+ \frac(16 )(9) \int\frac(dx)((x-1)^2)+ \frac(13)(54)\int\frac(dx)(x+2)=\\ &=\frac(41 )(108)\ln(x^2+2)- \frac(35)(27\sqrt(2))\název operátora (arctg)\frac(x)(\sqrt(2))- \frac(16) (9(x-1))+ \frac(13)(54) \ln|x+2|+C.\end(zarovnáno)
Integrování nesprávných zlomků
Předpokládejme, že potřebujeme integrovat funkci y=\frac(f(x))(g(x)), kde f(x) a g(x) jsou polynomy a stupeň polynomu f(x) je větší nebo roven stupni polynomu g(x) . V tomto případě musíte nejprve vybrat celou část nesprávného zlomku \frac(f(x))(g(x)), tj. reprezentovat jej ve tvaru
\frac(f(x))(g(x))=s(x)+ \frac(r(x))(g(x))\,
kde s(x) je polynom stupně rovný rozdílu mezi stupni polynomů f(x) a g(x) a \frac(r(x))(g(x))- správný zlomek.
Pak máme \int\frac(f(x))(g(x))\,dx= \int s(x)\,dx+ \int\frac(r(x))(g(x))\,dx\, ..
Příklad 5. Vypočítejme integrál nevlastního zlomku \int\frac(x^4-4x^3+x^2+16x-11)((x-1)(x+2)(x-3))\,dx.
Řešení. My máme:
\begin(aligned)g(x)&=(x-1)(x+2)(x-3)= x^3-2x^2-5x+6,\\ f(x)&=x^4 -4x^3+x^2+16x-11. \end (zarovnáno)
Chcete-li izolovat celou část, vydělte f(x) g(x): \frac(f(x))(g(x))= x-2+\frac(2x^2+1)(x^3-2x^2-5x+6)\,.
Prostředek, \int\frac(x^4-4x^3+x^2+16x-11)((x-1)(x+2)(x-3))\,dx= \int(x-2)dx+ \int\frac(2x^2+1)((x-1)(x+2)(x-3))\,dx
My máme: \int(x-2)dx=\frac(x^2)(2)-2x+C.
K výpočtu integrálu \int\frac(2x^2+1)((x-1)(x+2)(x-3))\,dx Je použita metoda neurčitých koeficientů, jak je uvedeno výše. Po výpočtech, které necháme na čtenáři, dostaneme.
Integrace racionálních funkcí Zlomek - racionální funkce Nejjednodušší racionální zlomky Rozklad racionálního zlomku na jednoduché zlomky Integrace jednoduchých zlomků Obecné pravidlo pro integraci racionálních zlomků
polynom stupně n. Zlomková - racionální funkce Zlomková - racionální funkce je funkce rovna poměru dvou polynomů: Racionální zlomek se nazývá vlastní, pokud je stupeň čitatele menší než stupeň jmenovatele, tj. m< n , в противном случае дробь называется неправильной. многочлен степени m Всякую неправильную рациональную дробь можно, путем деления числителя на знаменатель, представить в виде суммы многочлена L(x) и правильной рациональной дроби:)()()(x. Q x. P xf n m)()()(x. Q x. R x. L x. Q x. P
Zlomková - racionální funkce Redukujte nesprávný zlomek na správný tvar: 2 95 4 x xx 95 4 xx 2 x 3 x 34 2 xx 952 3 xx 2 2 x 23 42 xx 954 2 xx x 4 xx 84 2 93 x 3 63 x 15 2 95 4 x xx 342 23 xxx 2 15 x
Nejjednodušší racionální zlomky Vlastní racionální zlomky tvaru: Říká se jim nejjednodušší racionální zlomky typů. sekera A); 2(Nkk ax A k)04(2 2 qp qpxx NMx); 2; 04(2 2 Nkkqp qpxx NMx k V V,
Rozklad racionálního zlomku na jednoduché zlomky Věta: Libovolný správný racionální zlomek, jehož jmenovatel je faktorizován: lze navíc jedinečným způsobem znázornit ve formě součtu jednoduchých zlomků: s k qxpxxxxxx. Q)()()(22 2 11 2 21)()(x. Q x. P 1 xx A k k xx B)()(2 2 2 1 11 2 qxpx DCx 2 22 22 2 11) (qxpx Nx. M s ss qxpx Nx)
Rozklad racionálního zlomku na jednoduché zlomky Formulaci věty si vysvětlíme na následujících příkladech: K nalezení neurčitých koeficientů A, B, C, D... se používají dvě metody: metoda porovnávání koeficientů a metoda dílčích hodnot proměnné. Podívejme se na první metodu na příkladu. 3 2)3)(2(4 xx x 2 x A 3 3 2 21)3()3(3 x B x B 1 2 x DCx 22 22 2 11)1(1 xx Nx. M)1(3 22 3 xx x 2 21 x A 22 2)1)(4(987 xxx xx 4 x
Rozklad racionálního zlomku na jednoduché zlomky Zlomek uveďme jako součet jednoduchých zlomků: Přiveďme nejjednodušší zlomky ke společnému jmenovateli Srovnejme čitatele výsledného a původního zlomku Srovnejme koeficienty se stejnými mocninami x)52)(1( 332 2 2 xxx xx 1 x A 52 2 xx CBx )52)(1()1)(()52(2 2 xxx x. CBxxx. A 33252 222 xx. CBx. Cx. Bx. AAx. Ax 35 32 2 0 1 2 CAx BAx 2 3 1 C B A 52 23 1 1 2 xx x x
Integrace nejjednodušších zlomků Najděte integrály nejjednodušších racionálních zlomků: Podívejme se na integraci zlomků typu 3 na příkladu. dx ax A k dx qpxx NMx 2 ax axd A)(Cax. Aln)(axdax. A k C k ax. Ak
Integrace jednoduchých zlomkůdx xx x 102 13 2 dx xx x 9)12(13 2 dx x x 9)1(13 2 dtdx tx tx 1 1 dt t t 9 1)1 (3 2 dt t t 9 23 2 9 23 2 9 9 2 3 2 2 t td 33 2 t arctg. C t arctgt 33 2 9 ln 2 32 C x arctgxx 3 1 3 2 102 ln.
Integrace jednoduchých zlomků Integrál tohoto typu pomocí substituce: je redukován na součet dvou integrálů: První integrál se vypočítá zavedením t pod diferenciální znaménko. Druhý integrál se vypočítá pomocí vzorce opakování: dx qpxx NMx k 2 V t p x 2 kk při dt N při dtt M 22122 1221222))(1(222 321 kkkk atk t k k aat dt
Integrace jednoduchých zlomků a = 1; k = 3 323)1(t dt tarctg t dt 1 21)1)(12(2222 322 1 21222 t t t dt)1(22 1 2 t t t tarctg 2223)1)(13(2 2232 t2 3) Ct 1 (4)1(
Obecné pravidlo pro integrování racionálních zlomků Je-li zlomek nevlastní, reprezentujte jej jako součet polynomu a vlastního zlomku. Po faktorizaci jmenovatele správného racionálního zlomku jej představte jako součet jednoduchých zlomků s neurčitými koeficienty Najděte neurčité koeficienty metodou porovnávání koeficientů nebo metodou dílčích hodnot proměnné. Integrujte polynom a výsledný součet jednoduchých zlomků.
Příklad Uveďme zlomek ve správném tvaru. dx xxx 23 35 2 442 35 xxxxxx 23 2 2 x 345 2 xxx 442 34 xxx x 2 234 242 xxx 4425 23 xxx xxx 23 35 2 x 442 x 5 x 5 x 482 x 2 105 23 48 2 x x
Příklad Rozložme jmenovatel vlastního zlomku Rozložme zlomek jako součet jednoduchých zlomků Najděte neurčené koeficienty metodou parciálních hodnot proměnné xxx xx 23 2 2 48 2 2)1(48 xx xx 2 )1(1 x C x Š x A 2 2)1 ()1 (xx Cxx. Bxx. A 48)1()1 (22 xx. Cxx. Bxx. A 5241 31 40 CBAx Cx Ax 3 12 4 C B A xxx xx 23 2 2 48 2)1(3 1 124 xxx
Příklad dx xx 2 2)1(3 1 124 52 2 2)1(3 1 12452 x dx dxxdxdxx C x xxxx x 1 3 1 ln 12 ln
