γ+(90° +γ/2) =180°, což znamená γ = 60°. V tomto případě akordy O.A.
1
A OB 1
kružnice opsané čtyřúhelníku OA 1
NE 1
jsou stejné, protože mají stejné úhly OCA
1
A SŮL 1
.
Vepsaná kružnice Δ ABC ve vnitřních bodech se dotýká jejích stran. Pojďme zjistit, jaké kruhy se dotýkají tří čar AB, BC A SA. Střed kružnice tečné ke dvěma protínajícím se čarám leží na jedné ze dvou čar půlících úhly mezi původními čarami. Proto středy kružnic tečné k přímkám AB, BC A SA, leží na osách vnějších nebo vnitřních úhlů trojúhelníku (nebo jejich prodloužení). Osa vnitřního úhlu prochází průsečíkem libovolných dvou os vnějšího úhlu. Důkaz tohoto tvrzení doslovně opakuje důkaz odpovídajícího tvrzení pro osy vnitřních úhlů. Výsledkem jsou 4 kruhy se středy O, O A , Ach A O S
(obr. 57). Kruh se středem O A
se dotýká strany slunce A

pokračování stran AB A AC; tento kruh se nazývá nezapsáno
obvod Δ ABC. Poloměr kružnice trojúhelníku se obvykle označuje r a poloměry kružnic r A ,
G b a g S .
Mezi poloměry kružnice vepsané a kružnice platí následující vztahy:
G /
g s =(р-с)/р and G
G S =(p – a) (p – b), Kde R- poloobvod Δ ABC. Pojďme to dokázat. Nechť K a L jsou tečné body vepsaného a kružnice s přímkou slunce(obr. 58). Pravé trojúhelníky DŽUS A CO
C
L
jsou tedy podobné
G /
g s = OK/O S L
=
CK
/
C.L.
..
Dříve bylo prokázáno, že SC = (a+b-c)/2=p-c.
Zbývá to zkontrolovat C.L.
=
p
.
Nechat M A R- tečné body kružnice s přímkami AB A AC. Pak
CL= (CL+CP)/ 2 = (CB+BL+CA+AP)/2 = (CB+BM + CA+AM)/2 = R
Dokázat vztah rr
C
=(p
-
A
)(p
-
b
)
zvažte pravoúhlé trojúhelníky HLE.
C
B
A KVO, které jsou podobné, protože
<OBK
+<
Ó
C
B.L.
=(<СВА + <АВ
L
)/2 = 90°.
Prostředek, L O s /ВL =BK /KO, tzn. rr
C
=
K.O.
·
HLE.
C
=
B.K.
·
B.L.
.
Zbývá poznamenat, že VK=(A
+
C
-
b
)/2=
p
-
b
A B.L.
=
C.L.
-
C.B.
=
p
-
A
.
Všimněme si ještě jedné zajímavé vlastnosti (již vlastně cestou ověřené). Nechte vepsaný a kruhový kruh dotýkat se strany AB v bodech N A M(obr. 58). Pak DOPOLEDNE.
=
BN
.
Vskutku, BN
=
p
-
b
A AM=AR=SR-AS=p-c.
Poměry rr
C
=(p
- A)(p-PROTI )
A r
p=r
S (R-c) lze použít k odvození Heronova vzorce S
2
=
p
(p
-
A
)(p
-
b
)(p
-
C
),
Kde S
- oblast trojúhelníku. Vynásobením těchto poměrů dostaneme r
2
p
=(p
-
A
)(p
-
b
)(p
-
C
).
Zbývá to zkontrolovat S
=
pr
.
To lze snadno provést řezáním Δ ABC na ΔAOB,
ΔBOS A ΔSOA.

STŘEDNÍ Křižovatka
Dokažme, že se střednice trojúhelníku protínají v jednom bodě. Za tímto účelem zvažte bod M, kde se protínají mediány AA 1
A BB 1
.
Proveďme v Δ BB1S střední čára A
1
A
2
,
paralelní BB 1
(obr. 59). Pak A
1
M
:
DOPOLEDNE.
=
B
1
A
2
:
AB
1
=
B
1
A
2
:
B
1
C
=
B.A.
1
:VS=1:2, tj. průsečík mediánů BB 1
A AA 1
rozděluje medián AA 1
v poměru 1:2. Podobně průsečík střednic SS 1
A AA 1
rozděluje medián AA 1
v poměru 1:2. Tedy průsečík mediánů AA 1
A BB 1
se shoduje s průsečíkem mediánů AA 1
A SS 1
.
Pokud je průsečík střednic trojúhelníku připojen k vrcholům, pak se trojúhelník rozdělí na tři trojúhelníky o stejné ploše. Vskutku stačí dokázat, že pokud R- libovolný bod mediánu AA 1
PROTI ABC, pak oblast ΔAVR A ΔACP jsou rovny. Přece mediány AA 1
A RA 1
v Δ ABC a A RVS nakrájíme je na trojúhelníky o stejné ploše.
Platí i obrácené tvrzení: pokud pro nějaký bod R, ležící uvnitř Δ ABC, oblast Δ AVR, Δ
VE STŘEDU A ΔSAR jsou si tedy rovni R- průsečík mediánů. Vlastně z rovnosti oblastí ΔAVR A ΔHRV z toho vyplývá, že vzdálenosti od bodů A a C k přímce VR jsou si rovni, což znamená VR prochází středem segmentu AC. Pro AR A SR důkaz je podobný.
Rovnost ploch trojúhelníků, na které střednice rozdělují trojúhelník, nám umožňuje najít poměr ploch s trojúhelníku složeného z mediánů takto ΔABC, do oblasti S samotného Δ ABC. Nechat M- průsečík mediánů Δ ABC; tečka A" symetrický A vzhledem k bodu M(obr. 60)
Na jedné straně oblast ΔA"MS rovno S/3. Na druhou stranu je tento trojúhelník složen ze segmentů, z nichž délka je rovna 2/3 délky odpovídajícího mediánu, takže jeho plocha
rovno (2/3) 2 s = 4 s/9. Proto, s
=3
S
/4.

Velmi důležitou vlastností průsečíku mediánů je, že součet tří vektorů jdoucích z něj k vrcholům trojúhelníku je roven nule. Nejprve si to všimněme AM=1/3(AB+AC), Kde M- průsečík mediánů Δ
ABC
.
Ve skutečnosti, pokud
ABA
"S- tedy rovnoběžník AA"=AB+AC A AM = 1/3AA". Proto MA + MV + MC = 1/3 (BA + SA + AB + SV + AC + BC) = 0.
Je také jasné, že tuto vlastnost má pouze průsečík mediánů, protože pokud X
- tedy jakýkoli jiný bod
HA+XB+XC=(XM+MA)+(XM+MV)+(XM+MS)=3ХМ..
Pomocí této vlastnosti průsečíku střednic trojúhelníku můžeme dokázat následující tvrzení: průsečík střednic trojúhelníku s vrcholy ve středech stran AB,CD
A EF
šestiúhelník A B C D E F
shoduje se s průsečíkem střednic trojúhelníku s vrcholy ve středních bodech stran Slunce,DE
A F.A.
.
Ve skutečnosti s využitím toho, že pokud např. R- střed segmentu AB, pak pro jakýkoli bod X
rovnost je pravdivá HA+ HB=2ХР, lze snadno dokázat, že průsečíky mediánů obou uvažovaných trojúhelníků mají tu vlastnost, že součet vektorů jdoucích z nich k vrcholům šestiúhelníku je roven nule. Proto se tyto body shodují.
Průsečík střednic má jednu vlastnost, která jej ostře odlišuje od ostatních pozoruhodných bodů trojúhelníku: pokud Δ A"B"C" je projekce ΔABC na rovinu, pak průsečík mediánů Δ A "B" C"
je průmět průsečíku střednic ΔABC ve stejné rovině. To snadno vyplývá z toho, že při promítání jde střed úsečky do středu svého průmětu, což znamená, že medián trojúhelníku jde do mediánu jeho průmětu. Osa ani výška tuto vlastnost nemají.
Je třeba poznamenat, že průsečík střednic trojúhelníku je jeho těžiště, a to jak těžiště soustavy tří hmotných bodů se stejnou hmotností umístěných ve vrcholech trojúhelníku, tak těžiště trojúhelníku. deska ve tvaru daného trojúhelníku. Rovnovážná poloha trojúhelníku zavěšeného v libovolném bodě X
,
tam bude poloha, ve které paprsek HM směřující ke středu Země. Pro trojúhelník zavěšený v průsečíku mediánů je jakákoliv poloha rovnovážnou polohou. Navíc trojúhelník, jehož střední průsečík spočívá na špičce jehly, bude také v rovnovážné poloze.
VÝŠKOVÝ Křižovatka
Dokázat, že výšky Δ ABC protínají v jednom bodě, připomeňte si cestu důkazu naznačenou na konci části „Střed opsané kružnice“. Provedeme vás vrcholy A, B A S rovné čáry rovnoběžné s opačnými stranami; tyto čáry tvoří Δ A 1
V 1
S 1
(obr. 61). Výšky Δ ABC jsou kolmice ke stranám ΔA
1
B
1
C
1
.
V důsledku toho se protínají v jednom bodě - ve středu opsané kružnice ΔA
1
B
1
C
1
.
Průsečík výšek trojúhelníku se někdy nazývá jeho ortocentrum.
-
Je snadné zkontrolovat, že pokud H je průsečík výšek Δ ABC,Že A, B A S - výška průsečíků Δ VNS, ΔSNA a A ANV respektive.
To je také jasné<ABC
+ <
A.H.C.
=
180°, protože <
B.A.
1
H
= <
PŘED NAŠÍM LETOPOČTEM.
1
H
=90° (A
1
A C
1
- základny výšek). Pokud bod H
1
symetricky k bodu H vzhledem k přímce AC, pak čtyřúhelník ABCN 1
napsaný. Proto poloměry kružnic opsaných Δ ABC a A AN S jsou stejné a tyto kruhy jsou symetrické vzhledem ke straně AC(obr. 62). Nyní je snadné to dokázat
AN=a|ctg A|, kde a=BC. Vskutku,
AH = 2R hřích<
ACH = 2R|cos A| =a|ctg A| .
Předpokládejme pro jednoduchost, že ΔABC ostrý úhel a uvažujte Δ A
1
B
1
C
1
,
tvořené základnami jeho výšek. Ukazuje se, že střed vepsané kružnice Δ A
1
B
1
C
1
je průsečík výšek Δ ABC, a středy kruhů


ΔA
1
B
1
C
1
jsou vrcholy Δ ABC(obr. 63). Body A 1
A V 1
CH(od rohů NV 1
S a ON 1
S rovný), takže <
H.A.
1
B
1
= <
HCB
1
.
Rovněž<H.A.
1
C
1
= <
HBC
1
.
A od té doby<HCB
1
= =<
HBC
1
Že A 1
A - osy<V 1
A 1
S 1
.
Nechat N- průsečík výšek AA 1
, BB 1
A CC
1
trojúhelník ABC
.
Body A
1
A V 1
ležet na kruhu o průměru AB, Proto A.H.
·
A
1
H
=
B.H.
·
B
1
H
. Rovněž VNB
1
H
=CH.C 1
N.
Pro ostroúhlý trojúhelník platí i obrácené tvrzení: jestliže body A 1, B
1
A C
1
ležet po stranách VS, SA a AB s ostrým úhlem Δ ABC a segmenty AA 1
, BB 1
A SS 1
protínají v bodě R, a AR A 1
Р=ВР·В 1
P=SR·S 1
R,Že R- průsečík výšek. Vlastně z rovnosti
AP ·A 1 P =BP ·B 1 P
z toho vyplývá, že body A, B, A 1
A V 1
ležet na stejném kruhu s průměrem AB, což znamená <
AB
1
B
= <
B.A.
1
A
=γ.
Rovněž <
ACiC
=<
CAiA
=
β
A
<СВ
1
B=<ВС
1
C= α
(obr. 64). Je také zřejmé, že α + β= CC
1
A
=
l
80°, p+y = 180° a y + a = 180°. Proto α = β=γ=90°.
Průsečík výšek trojúhelníku lze určit ještě jiným velmi zajímavým způsobem, ale k tomu potřebujeme pojmy vektor a skalární součin vektorů.
Nechat O- střed kružnice opsané Δ ABC. Vektorový součet O A+ O.B.
+ OS je nějaký vektor, takže existuje takový bod R, Co NEBO = OA + OB + OS. Ukázalo se, že R- průsečík výšek Δ ABC!
Dokažme to například AP
kolmý PŘED NAŠÍM LETOPOČTEM.
.
To je jasné AR=AO+
+op=ao+(oa+ov+os)=ov+os a všechny= -ov+os.
Proto skalární součin vektorů AR A slunce rovná se OS 2
- O.B.
2
=
R
2
-
R
2
=0,
tj. tyto vektory jsou kolmé.
Tato vlastnost ortocentra trojúhelníku nám umožňuje dokázat některá zdaleka ne zřejmá tvrzení. Vezměme si například čtyřúhelník abeceda
,
vepsané do kruhu. Nechat Na, Nv, Ns A H
d
- ortocentra Δ
BCD
, Δ
CDA
, Δ
DAB
a A
ABC
respektive. Pak středy segmentů AN A , VN, CH S ,
D.H.
d
sladit se. Ve skutečnosti, pokud O je střed kruhu a M- střed segmentu AN A ,
Že OM = 1/2 (0A + OH A )= = 1/2 (OA + OB + OS + OD
)
.
Pro středy ostatních tří segmentů získáme přesně stejné výrazy.
EULER DIRECT
Nejúžasnější vlastností nádherných teček jeúhel spočívá v tom, že některé z nich jsou navzájem spojenyurčitými poměry. Například průsečík medián M,
průsečík výšek H a střed kružnice opsanévlastnosti O leží na stejné přímce a boduM rozděluje segment ON
aby vztah byl platnýOM:MN= 1:2. Tento věta byla prokázána v roce 1765 Leonhardem Eulerem, kterýSvou neúnavnou činností významně rozvinul mnohé oblasti matematiky a položil základy mnoha jejím novým oborům. Narodil se roku 1707 ve Švýcarsku. Euler doporučil ve věku 20 letBratři Bernoulliové dostali pozvání do Petrohraduburg, kde byla krátce předtím uspořádána akademie. Vkoncem roku 1740 v Rusku v souvislosti s nástupem Anny Leopolové k mociDovna, došlo k alarmující situaci a Euler se přestěhovalBerlín. Po 25 letech se vrátil do Ruska znovu, celkemEuler žil v Petrohradě více než 30 let. Zatímco v Burleyne, Euler udržoval úzký kontakt s Ruskou akademií a byljeho čestným členem. Z Berlína si Euler dopisoval s Lomonemsovy Jejich korespondence začala následovně. V roce 1747 byl Lomonosov zvolen profesorem, tedy řádným členem akademie; Císařovna tuto volbu schválila. Potomreakční úředník Akademie Schumacher, který vehementně nenávidí PrávoMonosov, poslal svou práci Eulerovi v naději, že o nich získá informacešpatná recenze. (Euler byl jen o 4 roky starší než Lomonosov,ale jeho vědecká autorita byla v té době již velmi vysoká.)Euler ve své recenzi napsal: „Všechna tato díla nejsou jen dobráshi, ale také vynikající, protože vysvětluje fyzikální a chemické nejnutnější a nejtěžší záležitosti, které jsou zcela neznámé a interpretace byly nemožnétěm nejdůvtipnějším a nejučenějšímslavných lidí s takovým zakladatelemvěc, kterou jsem si docela jistýpřesnost jeho důkazů...Člověk si musí přát všechnoKteré akademie dokázaly ukázat takové vynálezy, žekteré pan Lomo ukázal nosy."
Přejděme k důkazu Eulerova věta. Uvažujme Δ
A
1
B
1
C
1
s vrcholy dovnitř  středy stran Δ ABC; nechat H
1
a H - jejich ortocentra (obr. 65). Bod H 1 se shoduje se středem O kružnice opsané Δ ABC. Dokažme, že Δ C
1
H
1
M
=Δ
CHM
.
Vlastně vlastností průsečíku mediánů S 1
M:
CM= 1:2, koeficient podobnosti Δ A
1
B
1
C
1
a A ABC se rovná 2, takže C
1
H
1
:
CH
=1:2,
Kromě,<H
1
C
1
M
=<НСМ (C
1
H
1
||
CH
).
Proto,< C
1
M.H.
1
= < SMN, což znamená bod M leží na segmentu H
1
H
.
Kromě, H
1
M
:
M.H.
=1:2,
protože koeficient podobnosti Δ C
1
H
1
M
a A SNM rovná se 2.
středy stran Δ ABC; nechat H
1
a H - jejich ortocentra (obr. 65). Bod H 1 se shoduje se středem O kružnice opsané Δ ABC. Dokažme, že Δ C
1
H
1
M
=Δ
CHM
.
Vlastně vlastností průsečíku mediánů S 1
M:
CM= 1:2, koeficient podobnosti Δ A
1
B
1
C
1
a A ABC se rovná 2, takže C
1
H
1
:
CH
=1:2,
Kromě,<H
1
C
1
M
=<НСМ (C
1
H
1
||
CH
).
Proto,< C
1
M.H.
1
= < SMN, což znamená bod M leží na segmentu H
1
H
.
Kromě, H
1
M
:
M.H.
=1:2,
protože koeficient podobnosti Δ C
1
H
1
M
a A SNM rovná se 2.
KRUH DEVĚTI BODŮ
V roce 1765 Euler zjistil, že středy stran trojúhelníku a základny jeho výšek leží na stejné kružnici. Tuto vlastnost trojúhelníku také prokážeme.
Nechť B 2 je základna výšky svržené shora V na
boční AC. Body V a B2 jsou symetrické kolem přímky A 1
S 1
(obr. 66). Proto Δ A
1
V
2
S
1
= Δ
A
1
PŘED NAŠÍM LETOPOČTEM.
t
= Δ
A
1
B
1
C
1
,
Proto <
A
1
B
2
C
1
= <А
1
V 1
S 1
,
což znamená bod V 2
leží na popsaném
kruh ΔA
1
V
1
S
1
.
Pro zbývající základny výšek je důkaz podobný. „

Následně se zjistilo, že na stejné kružnici leží další tři body – středy úseček spojujících ortocentrum s vrcholy trojúhelníku. Tak to je kruh devíti bodů.
Nechat Az A SZ- středy segmentů AN A CH, S 2
- základna výšky klesla shora S na AB(obr. 67). Nejprve to dokažme A
1
C
1
A
3
C
3
- obdélník. To snadno vyplývá z toho, že A 1
SZ A A
3
C
1
- středové čáry Δ VSN A ΔAVN, A A
1
C
1
A A 3
SZ- středové čáry Δ ABC a A ASN. Proto ty body A 1
A Az ležet na kruhu o průměru S 1
SZ, a od té doby Az A SZ leží na kružnici procházející body A 1,
C
1
a C2. Tato kružnice se shoduje s kružnicí uvažovanou Eulerem (pokud Δ ABC ne rovnoramenné). Za bod Vz důkaz je podobný.
TORRICELLI BOD
Uvnitř libovolného čtyřúhelníku abeceda
Je snadné najít bod, jehož součet vzdáleností k vrcholům má nejmenší hodnotu. Takový bod je bod O průsečík jeho úhlopříček. Ve skutečnosti, pokud X
- tedy jakýkoli jiný bod AH+HS≥AC=AO+OS A BX
+
XD
≥
BD
=
B.O.
+
O.D.
,
a alespoň jedna z nerovností je přísná. U trojúhelníku se podobný problém řeší obtížněji, nyní přejdeme k jeho řešení. Pro jednoduchost budeme uvažovat případ ostrého trojúhelníku.
Nechat M- nějaký bod uvnitř ostrého úhlu Δ ABC. Otočme to Δ ABC spolu s tečkou M 60° kolem bodu A(obr. 68). (Přesněji, nech PŘED NAŠÍM LETOPOČTEM A M"- obrázky bodů PŘED NAŠÍM LETOPOČTEM A M při otočení o 60° kolem bodu A.) Pak AM+VM+SM=MM"+B.M.
+
C
"
M
", AM=MM", Tak jako ΔAMM"- rovnoramenný (AM=AM") A<MAM" = 60°. Pravá strana rovnosti je délka přerušované čáry VMM"S"
;
bude nejmenší, když tato přerušovaná čára

se shoduje se segmentem slunce"
.
V tomto případě<.
A.M.B.
=
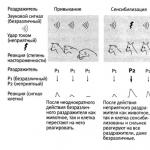
180° -<AMM" = 120° a<АМС = <DOPOLEDNE.
"
C
-
180°-<DOPOLEDNE.
"
M
=
120°, tedy strany AB, BC a SA jsou viditelné z bodu M pod úhlem 120°. Takový bod M volal Torricelliho bod trojúhelník ABC
.
Dokažme však, že uvnitř ostroúhlého trojúhelníku vždy existuje bod M, ze kterého je každá strana viditelná pod úhlem 120°. Postavíme to na stranu AB trojúhelník ABC
zevně správné Δ ABC 1
(obr. 69). Nechat M-průsečík kružnice opsané ΔABC 1
a rovný SS 1
.
Pak ABC
1
= 60° A ABC viditelné z bodu M pod úhlem 120°. Pokračujeme-li v těchto argumentech o něco dále, můžeme získat další definici Torricelliho bodu. Postavíme pravidelné trojúhelníky A 1
slunce A AB 1
S i na stranách ozbrojených sil a AC. Dokažme, že bod M také leží na přímce AA 1
.
Opravdu, tečka M leží na kružnici opsané Δ A
1
PŘED NAŠÍM LETOPOČTEM.
,
Proto<A
1
M.B.
= <
A
1
C.B.
= 60°, což znamená<A 1
MV+<.
B.M.A.
=
180°. Stejně tak bod M leží na přímce BB 1
(obr. 69).
Uvnitř Δ ABC existuje jediný bod M, ze kterého jsou jeho strany viditelné pod úhlem 120°, protože opsané kružnice Δ ABC
1
, Δ
AB
i
C
a A A
1
slunce nemůže mít více než jeden společný bod.
Uveďme nyní fyzikální (mechanický) výklad Torricelliho bodu. Upravme Δ ve vrcholech ABC kroužky, provlečeme jimi tři lana, jejichž jeden konec je svázán a na druhé konce jsou připevněny břemena stejné hmotnosti (obr. 70). Li x = MA, y = MV,z
=
M.C.
A A je délka každého vlákna, pak se potenciální energie uvažovaného systému rovná m G
(X
-A)+ m G
(y
-
A
)+
mg
(z
--A). V rovnovážné poloze má potenciální energie nejmenší hodnotu, takže nejmenší hodnotu má i součet x+y+z. Na druhé straně v rovnovážné poloze je výslednice sil v bodě M rovna nule. Tyto síly jsou stejné v absolutní velikosti, proto párové úhly mezi silovými vektory jsou rovny 120°.

Zbývá říci, jak se věci mají v případě tupého trojúhelníku. Pokud je tupý úhel menší než 120°, pak všechny předchozí argumenty zůstávají platné. A pokud je tupý úhel větší nebo roven 120°, pak součet vzdáleností od bodu trojúhelníku k jeho vrcholům bude nejmenší, když je tento bod vrcholem tupého úhlu.
BROKARDOVY BODY
Brocard body Δ ABC takové vnitřní body se nazývají R A Q
,
Co<ABP
= <.
BCP
=<
VÍČKO
A<.
QAB
= <.
QBC
= < QCA
(u rovnostranného trojúhelníku se body Brocard spojí do jednoho bodu). Dokažme, že uvnitř libovolného Δ ABC tam je bod R, mající požadovanou vlastnost (pro bod Q
důkaz je podobný). Nejprve zformulujme definici Brocardova bodu v jiné podobě. Označme hodnoty úhlu podle obrázku 71. Od<ARV=180° - a+x-y, rovnost x=y je ekvivalentní rovnosti<APB
=180°-<
.
A
.
Proto, R- bod Δ ABC, z jakých stran AB,
slunce A SA viditelné pod úhlem 180° -<.
A
,
180°-<B
,
180°-<S.
Takový bod lze zkonstruovat následovně. Pojďme stavět dál
boční slunce trojúhelník ABC podobný trojúhelník CA1B
jak je znázorněno na obrázku 72. Dokažme, že bod P průsečíku přímky AA1 a okroužkujte ΔA1BC hledaný. Ve skutečnosti,<BPC
=18
Ó
° - β
A<APB
=
180°-<A
t
P.B.
=
180° -<A
1
C.B.
=
l
80°- A. Sestrojme dále podobné trojúhelníky na stranách podobným způsobem AC A AB(obr. 73). Protože<.
APB
=
180° - A, tečka R také leží na kružnici opsané Δ ABC 1
Proto,<BPC
1
= <BAC
1
= β, což znamená bod
R leží na segmentu SS 1
.
Podobně leží na segmentu BB 1
,
tj. R - průsečík segmentů AA 1
, BB 1
A SS 1
.
Brocard bod R má následující zajímavou vlastnost. Nechte rovnou AR, VR A SR protínají kružnici opsanou ΔABC


v bodech A 1, B 1 a C 1 (obr. 74). Potom Δ ABC = Δ
B
1
S 1
A
1
.V ve skutečnosti,<.
A
1
B
1
C
1
= <
A
1
B
1
B
+ <
BB1C1=<A
1
AB
+<В
CC 1 =<A
1
AB
+ +<
A
1
A.C.
=<.ВАС,
díky vlastnosti Brocardova bodu ΔABC jsou úhly BCC 1 a A 1 AC stejné, což znamená A
1
C
1
=
PŘED NAŠÍM LETOPOČTEM.
.
Rovnost zbývajících stran Δ ABC a Δ B 1 C 1 A 1 jsou kontrolovány stejným způsobem.
Ve všech případech, které jsme uvažovali, lze důkaz, že se odpovídající trojice čar protínají v jednom bodě, provést pomocí Cevova věta. Tuto větu zformulujeme.
Teorém. Nechte po stranách AB, BC A S A trojúhelník ABC
získané body S 1
, A 1
A V 1
respektive. Přímo AA 1
, BB 1
A SS 1
protínají v jednom bodě tehdy a jen tehdy
AC 1 / C 1 V VA 1 / A 1 C SV 1 / V 1 A = 1.
Důkaz věty je uveden v učebnici geometrie pro ročníky 7-9 od L.S.
Literatura.
1.Atanasyan L.S. Geometrie 7-9.- M.: Vzdělávání, 2000.
2. Kiselev A.P. Elementární geometrie - M.: Vzdělávání, 1980.
3. Nikolskaya I.L. Volitelný kurz matematiky. M.: Vzdělávání, 1991.
4. Encyklopedický slovník mladého matematika... Komp. A.P.Savin.-.M.: Pedagogika, 1989.
Ministerstvo všeobecného a odborného vzdělávání Sverdlovské oblasti.
Městská vzdělávací instituce v Jekatěrinburgu.
Vzdělávací instituce – MOUSOSH č. 212 „Jekatěrinburské kulturní lyceum“
Vzdělávací obor – matematika.
Předmět - geometrie.
Pozoruhodné body trojúhelníku
Referent: Žák 8. třídy
Selitsky Dmitrij Konstantinovič.
Vědecký poradce:
Rabkanov Sergej Petrovič.
Jekatěrinburg, 2001
Úvod 3
Popisná část:
Ortocentrum 4
Střed 5
Těžiště 7
Circumcenter 8
Eulerova řada 9
Praktická část:
Ortocentrický trojúhelník 10
Závěr 11
Reference 11
Úvod.
Geometrie začíná trojúhelníkem. Po dvě a půl tisíciletí je trojúhelník symbolem geometrie. Jeho nové vlastnosti jsou neustále objevovány. Mluvit o všech známých vlastnostech trojúhelníku zabere hodně času. Zajímaly mě takzvané „pozoruhodné body trojúhelníku“. Příkladem takových bodů je průsečík os. Pozoruhodné na tom je, že když vezmete tři libovolné body v prostoru, sestrojíte z nich trojúhelník a nakreslíte osy, pak se (sektory) protnou v jednom bodě! Zdálo by se, že to není možné, protože jsme brali libovolné body, ale toto pravidlo platí vždy. Ostatní „pozoruhodné body“ mají podobné vlastnosti.
Po přečtení literatury na toto téma jsem si opravil definice a vlastnosti pěti nádherných bodů a trojúhelníku. Moje práce tím ale neskončila; chtěl jsem tyto body prozkoumat sám.
Proto cílová Tato práce je studiem některých pozoruhodných vlastností trojúhelníku a studiem ortocentrického trojúhelníku. V procesu dosažení tohoto cíle lze rozlišit následující fáze:
Výběr literatury s pomocí učitele
Studium základních vlastností pozoruhodných bodů a čar trojúhelníku
Zobecnění těchto vlastností
Sestavení a řešení problému zahrnujícího ortocentrický trojúhelník
Prezentoval jsem výsledky získané v této výzkumné práci. Všechny kresby jsem vytvořil pomocí počítačové grafiky (vektorový grafický editor CorelDRAW).
Ortocentrum. (průsečík výšek)
Dokažme, že se výšky protínají v jednom bodě. Provedeme vás vrcholy A, V A S trojúhelník ABC rovné čáry rovnoběžné s opačnými stranami. Tyto čáry tvoří trojúhelník A 1
V 1
S 1
. výška trojúhelníku ABC jsou odvěsny ke stranám trojúhelníku A 1
V 1
S 1
. proto se protínají v jednom bodě - ve středu kružnice opsané trojúhelníku A 1
V 1
S 1
. Průsečík výšek trojúhelníku se nazývá ortocentrum ( H).
Icentrum je střed vepsané kružnice.
(Bod průsečíku os)

Dokažme, že osy úhlů trojúhelníku ABC protínají v jednom bodě. Zvažte pointu O průsečíky úhlových os A A V. všechny body osy úhlu A jsou stejně vzdálené od přímek AB A AC a libovolný bod osy úhlu V ve stejné vzdálenosti od přímek AB A slunce, takže bod O ve stejné vzdálenosti od přímek AC A slunce, tj. leží na ose úhlu S. tečka O ve stejné vzdálenosti od přímek AB,
slunce A SA, což znamená, že existuje kruh se středem O, tečné k těmto přímkám a tečné body leží na samotných stranách a ne na jejich prodlouženích. Ve skutečnosti úhly ve vrcholech A A V trojúhelník AOB ostrý tedy projekční bod O přímo AB leží uvnitř segmentu AB.
Na večírky slunce A SA důkaz je podobný.
Icenter má tři vlastnosti:

Je-li pokračování osy úhlu S protíná kružnici opsanou trojúhelníku ABC na místě M, Že MA=MV=MO.

Li AB- základna rovnoramenného trojúhelníku ABC, pak kružnici tečnou ke stranám úhlu DIA v bodech A A V, prochází bodem O.

Pokud přímka procházející bodem O rovnoběžně se stranou AB, překračuje strany slunce A SA v bodech A 1
A V 1
, Že A 1
V 1
=A 1
V+AB 1
.
Centrum gravitace. (průsečík mediánů)

Dokažme, že se střednice trojúhelníku protínají v jednom bodě. Za tímto účelem zvažte bod M, ve kterém se protínají mediány AA 1
A BB 1
. nakreslíme trojúhelník BB 1
S střední čára A 1
A 2
, paralelní BB 1
. Pak A 1
M: AM=V 1
A 2
:AB 1
=V 1
A 2
:V 1
S=VA 1
:SLUNCE= 1:2, tzn. střední průsečík BB 1
A AA 1
rozděluje medián AA 1
v poměru 1:2. Podobně průsečík střednic SS 1
A AA 1
rozděluje medián AA 1
v poměru 1:2. Tedy průsečík mediánů AA 1
A BB 1
se shoduje s průsečíkem mediánů AA 1
A SS 1
.
Pokud je průsečík střednic trojúhelníku připojen k vrcholům, pak se trojúhelníky rozdělí na tři trojúhelníky o stejné ploše. Vskutku stačí dokázat, že pokud R– libovolný bod mediánu AA 1
v trojúhelníku ABC, pak plochy trojúhelníků AVR A AKT jsou rovny. Přece mediány AA 1
A RA 1
v trojúhelnících ABC A RVS nakrájíme je na trojúhelníky o stejné ploše.
Platí i obrácené tvrzení: pokud pro nějaký bod R, ležící uvnitř trojúhelníku ABC, oblast trojúhelníků AVR, VE STŘEDU A SAR jsou si tedy rovni R– průsečík mediánů.
Průsečík má ještě jednu vlastnost: pokud vyříznete trojúhelník z libovolného materiálu, nakreslíte na něj střednice, připevníte tyč v průsečíku střednic a zajistíte zavěšení na stativu, pak bude model (trojúhelník) ve rovnovážný stav, proto průsečík není nic jiného než těžiště trojúhelníku.
Střed opsané kružnice.

Dokažme, že existuje bod stejně vzdálený od vrcholů trojúhelníku, nebo jinými slovy, že třemi vrcholy trojúhelníku prochází kružnice. Umístění bodů stejně vzdálené od bodů A A V, je kolmá k segmentu AB, procházející jeho středem (kolmice k segmentu AB). Zvažte pointu O, ve kterém se protínají osy kolmiček na úsečky AB A slunce. Tečka O stejně vzdálené od bodů A A V, stejně jako z bodů V A S. proto je ve stejné vzdálenosti od bodů A A S, tj. také leží na kolmici k úsečce AC.
Centrum O kružnice opsaná leží uvnitř trojúhelníku pouze tehdy, je-li trojúhelník ostroúhlý. Pokud je trojúhelník pravoúhlý, pak bod O shoduje se se středem přepony, a je-li úhel ve vrchol S tupé, pak rovné AB odděluje body O A S.

V matematice se často stává, že objekty definované zcela odlišnými způsoby se ukáží jako stejné. Ukažme si to na příkladu.
Nechat A 1
,
V 1
,S 1
– středy stran slunce,SA a AB. Lze prokázat, že opsané kružnice trojúhelníků AB 1
S,
A 1
slunce 1
A A 1
V 1
S 1
protínají v jednom bodě a tento bod je středem obvodu trojúhelníku ABC. Máme tedy dva zdánlivě zcela odlišné body: průsečík odvěsnic ke stranám trojúhelníku ABC a průsečíkem opsaných kružnic trojúhelníků AB 1
S 1
,
A 1
slunce A A 1
V 1
S 1
. ale ukázalo se, že tyto dva body se shodují.
Eulerova přímka.

Nejúžasnější vlastností pozoruhodných bodů trojúhelníku je, že některé z nich jsou navzájem spojeny určitými vztahy. Například těžiště M, ortocentrum N a středem opsaného kruhu O leží na stejné přímce a bod M rozděluje úsečku OH tak, aby vztah byl platný OM: MN= 1:2. Tuto větu dokázal v roce 1765 švýcarský vědec Leonardo Euler.
Ortocentrický trojúhelník.

Ortocentrický trojúhelník(pravoúhlý trojúhelník) je trojúhelník ( MNNA), jehož vrcholy jsou základnami nadmořských výšek tohoto trojúhelníku ( ABC). Tento trojúhelník má mnoho zajímavých vlastností. Dejme jeden z nich.
Vlastnictví.
Dokázat:
Trojúhelníky AKM, CMN A BKN podobný trojúhelníku ABC;
Úhly pravoúhlého trojúhelníku MNK jsou: L
KNM
= π - 2
L
A,LKMN
=
π – 2 L
B,
L
MNK
= π - - 2 L
C.
Důkaz:
My máme AB cos A, A.K. cos A. Proto, DOPOLEDNE./AB
= A.K./A.C..
Protože u trojúhelníků ABC A AKM roh A– společné, pak jsou podobné, z čehož usuzujeme, že úhel L
AKM
= L
C. Proto L
BKM
= L
C. Dále máme L
MKC= π/2 – L
C, L
NKC= π/2 – – – L
C, tj. SK– úsečka úhlu MNK. Tak, L
MNK= π – 2 L
C. Zbývající rovnosti jsou prokázány podobně.
Závěr.
Na konci této výzkumné práce lze vyvodit následující závěry:
Pozoruhodné body a čáry trojúhelníku jsou:
ortocentrum trojúhelníku je průsečík jeho výšek;
a střed trojúhelník je průsečík os;
centrum gravitace trojúhelníku je průsečík jeho mediánů;
circumcenter– je průsečík kolmiček os;
Eulerova přímka- to je přímka, na které leží těžiště, ortocentrum a střed kružnice opsané.
Ortocentrický trojúhelník rozděluje daný trojúhelník na tři podobné.
Po této práci jsem se naučil hodně o vlastnostech trojúhelníku. Tato práce pro mě byla relevantní z hlediska rozvoje mých znalostí v oblasti matematiky. V budoucnu hodlám toto zajímavé téma rozvíjet.
Bibliografie.
Kiselyov A.P. Elementární geometrie. – M.: Vzdělávání, 1980.
Coxeter G.S., Greitzer S.L. Nová setkání s geometrií. – M.: Nauka, 1978.
Prasolov V.V. Problémy v planimetrii. – M.: Nauka, 1986. – 1. díl.
Sharygin I.F. Geometrické úlohy: Planimetrie. – M.: Nauka, 1986.
Scanavi M.I. Problémy s řešením. – Rostov na Donu: Phoenix, 1998.
Berger M. Geometrie ve dvou svazcích - M: Mir, 1984.
Obsah
Úvod……………………………………………………………………………………………… 3
Kapitola 1.
1.1 Trojúhelník………………………………………………………………………………………..4
1.2.
Mediány trojúhelníku
1.4. Výšky v trojúhelníku
Závěr
Seznam použité literatury
Brožur
Úvod
Geometrie je obor matematiky, který se zabývá různými útvary a jejich vlastnostmi. Geometrie začíná trojúhelníkem. Po dvě a půl tisíciletí byl trojúhelník symbolem geometrie; ale není to jen symbol, trojúhelník je atom geometrie.
Ve své práci se budu zabývat vlastnostmi průsečíků os, mediánů a výšek trojúhelníku a budu mluvit o jejich pozoruhodných vlastnostech a přímkách trojúhelníku.
Mezi takové body studované ve školním kurzu geometrie patří:
a) průsečík os (střed vepsané kružnice);
b) průsečík odvěsnic os (střed opsané kružnice);
c) průsečík výšek (orthocentrum);
d) průsečík mediánů (těžiště).
Relevantnost:
rozšířit své znalosti o trojúhelníku,jeho vlastnostiúžasné body.
Cílová:
průzkum trojúhelníku k jeho pozoruhodným bodům,studovat jeklasifikace a vlastnosti.
úkoly:
1. Prostudujte si potřebnou literaturu
2. Prostudujte si klasifikaci pozoruhodných bodů trojúhelníku
3. Umět sestrojit pozoruhodné trojúhelníkové body.
4. Shrňte nastudovaný materiál pro návrh brožury.
Hypotéza projektu:
schopnost najít pozoruhodné body v jakémkoli trojúhelníku umožňuje řešit geometrické konstrukční problémy.
Kapitola 1.
Historické informace o pozoruhodných bodech trojúhelníku
Ve čtvrté knize Elements Euklides řeší problém: "Vepsat kruh do daného trojúhelníku." Z řešení vyplývá, že tři osy vnitřních úhlů trojúhelníku se protínají v jednom bodě - středu vepsané kružnice. Z řešení dalšího euklidovského problému vyplývá, že kolmice obnovené ke stranám trojúhelníku v jejich středech se také protínají v jednom bodě - středu opsané kružnice. Elementy neříkají, že se tři výšky trojúhelníku protínají v jednom bodě, který se nazývá ortocentrum (řecké slovo „orthos“ znamená „rovný“, „správný“). Tento návrh však znali Archimedes, Pappus a Proclus.
Čtvrtý singulární bod trojúhelníku je průsečík střednic. Archimédes dokázal, že je to těžiště (barycentrum) trojúhelníku. Výše uvedeným čtyřem bodům byla věnována zvláštní pozornost a od 18. století se jim říkalo „pozoruhodné“ nebo „zvláštní“ body trojúhelníku.
Studium vlastností trojúhelníku spojených s těmito a dalšími body posloužilo jako počátek pro vytvoření nového odvětví elementární matematiky - „geometrie trojúhelníku“ nebo „nové geometrie trojúhelníku“, jehož jedním ze zakladatelů byl Leonhard Euler. V roce 1765 Euler dokázal, že v každém trojúhelníku leží orthocenter, barycenter a circumcenter na stejné přímce, později nazývané „Eulerova přímka“.
Trojúhelník
Trojúhelník
- geometrický obrazec sestávající ze tří bodů, které neleží na stejné přímce, a tří segmentů spojujících tyto body ve dvojicích. Body -vrcholy
trojúhelník, segmenty -strany
trojúhelník.
V
A, B, C - vrcholy
AB, BC, SA - strany
A C
Ke každému trojúhelníku jsou přidruženy čtyři body:
Průsečík střednic;
Průsečík průsečíků;
Průsečík výšek.
Průsečík odvěsných os;
1.2.
Mediány trojúhelníku
Medina trojúhelníku - , spojující vrchol ze středu protější strany (obrázek 1). Bod, kde střed protíná stranu trojúhelníku, se nazývá základna mediánu.

Obrázek 1. Mediány trojúhelníku
Vytvořme středy stran trojúhelníku a nakreslete segmenty spojující každý z vrcholů se středem protější strany. Takové segmenty se nazývají mediány.
A opět pozorujeme, že se tyto segmenty protínají v jednom bodě. Pokud měříme délky výsledných středních segmentů, můžeme zkontrolovat ještě jednu vlastnost: průsečík mediánů rozděluje všechny mediány v poměru 2:1, počítáno od vrcholů. A přesto je trojúhelník, který spočívá na špičce jehly v průsečíku mediánů, v rovnováze! Bod s touto vlastností se nazývá těžiště (barycenter). Střed o stejné hmotnosti se někdy nazývá těžiště. Vlastnosti mediánů trojúhelníku lze tedy formulovat následovně: mediány trojúhelníku se protínají v těžišti a jsou děleny průsečíkem v poměru 2:1, počítáno od vrcholu.
1.3. Osy trojúhelníku
Bisector volal osa úhlu vedeného od vrcholu úhlu k jeho průsečíku s protější stranou. Trojúhelník má tři osy odpovídající jeho třem vrcholům (obrázek 2).

Obrázek 2. Osa trojúhelníku
V libovolném trojúhelníku ABC nakreslíme osy jeho úhlů. A opět, při přesné konstrukci se všechny tři osy protnou v jednom bodě D. Bod D je také neobvyklý: je stejně vzdálený od všech tří stran trojúhelníku. To lze ověřit sklopením kolmiček DA 1, DB 1 a DC1 ke stranám trojúhelníku. Všechny jsou si navzájem rovny: DA1=DB1=DC1.
Pokud nakreslíte kružnici se středem v bodě D a poloměrem DA 1, pak se bude dotýkat všech tří stran trojúhelníku (to znamená, že s každou z nich bude mít pouze jeden společný bod). Takový kruh se nazývá vepsaný do trojúhelníku. Osy úhlů trojúhelníku se tedy protínají ve středu vepsané kružnice.
1.4. Výšky v trojúhelníku
Výška trojúhelníku - , spadl z vrcholu na opačnou stranu nebo přímku shodující se s opačnou stranou. V závislosti na typu trojúhelníku může být výška obsažena v trojúhelníku (např trojúhelník), shodují se s jeho stranou (být trojúhelník) nebo procházet mimo trojúhelník v tupoúhlém trojúhelníku (obrázek 3).



Obrázek 3. Výšky v trojúhelnících
Pokud sestrojíte tři výšky v trojúhelníku, pak se všechny protnou v jednom bodě H. Tento bod se nazývá ortocentrum. (Obrázek 4).
Pomocí konstrukcí můžete zkontrolovat, že v závislosti na typu trojúhelníku je ortocentrum umístěno odlišně:
pro ostrý trojúhelník - uvnitř;
pro obdélníkový - na přeponu;
pro tupý úhel je na vnější straně.

Obrázek 4. Ortocentrum trojúhelníku
Tak jsme se seznámili s dalším pozoruhodným bodem trojúhelníku a můžeme říci, že: výšky trojúhelníku se protínají v ortocentru.
1.5. Kolmice osy ke stranám trojúhelníku
Kolmice úsečky je úsečka kolmá k dané úsečce a procházející jejím středem.
Narýsujme libovolný trojúhelník ABC a na jeho strany nakreslete odvěsny. Pokud je konstrukce provedena přesně, pak se všechny kolmice protnou v jednom bodě - bodě O. Tento bod je stejně vzdálený od všech vrcholů trojúhelníku. Jinými slovy, nakreslíte-li kružnici se středem v bodě O, procházející jedním z vrcholů trojúhelníku, pak bude procházet i jeho dalšími dvěma vrcholy.
Kruh procházející všemi vrcholy trojúhelníku se nazývá opsaný kolem něj. Stanovenou vlastnost trojúhelníku lze tedy formulovat následovně: odvěsny ke stranám trojúhelníku se protínají ve středu kružnice opsané (obrázek 5).
 Obrázek 5. Trojúhelník vepsaný do kruhu
Obrázek 5. Trojúhelník vepsaný do kruhu
Kapitola 2. Studium pozoruhodných bodů trojúhelníku.
Studium výšky v trojúhelníku
Všechny tři výšky trojúhelníku se protínají v jednom bodě. Tento bod se nazývá ortocentrum trojúhelníku.

Nadmořské výšky ostrého trojúhelníku jsou umístěny přesně uvnitř trojúhelníku.
Podle toho je průsečík výšek také umístěn uvnitř trojúhelníku.
V pravoúhlém trojúhelníku se dvě výšky shodují se stranami. (Jsou to výšky nakreslené od vrcholů ostrých úhlů k nohám).
Výška nakreslená k přeponě leží uvnitř trojúhelníku.
AC je výška nakreslená od vrcholu C ke straně AB.
AB je výška nakreslená od vrcholu B ke straně AC.
AK je výška vedená od vrcholu pravého úhlu A k přeponě BC.
Výšky pravoúhlého trojúhelníku se protínají ve vrcholu pravého úhlu (A je ortocentrum).
V tupoúhlém trojúhelníku je uvnitř trojúhelníku pouze jedna nadmořská výška – ta nakreslená z vrcholu tupého úhlu.
Další dvě výšky leží mimo trojúhelník a jsou sníženy na pokračování stran trojúhelníku.
AK je výška nakreslená na stranu BC.
BF - výška nakreslená na pokračování strany AC.
CD je výška nakreslená k pokračování strany AB.
Průsečík výšek tupého trojúhelníku je také mimo trojúhelník:
H je ortocentrum trojúhelníku ABC.
Studium os v trojúhelníku
Osa trojúhelníku je část osy úhlu trojúhelníku (paprsku), která je uvnitř trojúhelníku.
 Všechny tři osy trojúhelníku se protínají v jednom bodě.
Všechny tři osy trojúhelníku se protínají v jednom bodě.


Průsečík os v ostroúhlém, tupém a pravoúhlém trojúhelníku je středem vepsané kružnice v trojúhelníku a nachází se uvnitř.
Studium mediánů v trojúhelníku
Protože trojúhelník má tři vrcholy a tři strany, existují také tři segmenty spojující vrchol a střed protilehlé strany.



Po prozkoumání těchto trojúhelníků jsem si uvědomil, že v jakémkoli trojúhelníku se mediány protínají v jednom bodě. Tento bod se nazývá těžiště trojúhelníku.
Studium odvěsnic ke straně trojúhelníku
Kolmice
trojúhelníku je kolmice nakreslená ke středu strany trojúhelníku.


Tři kolmé osy trojúhelníku se protínají v jednom bodě a jsou středem kružnice opsané.
Průsečík odvěsných os v ostroúhlém trojúhelníku leží uvnitř trojúhelníku; v tupém úhlu - mimo trojúhelník; v pravoúhlém - uprostřed přepony.
Závěr
V průběhu práce dojdeme k následujícím závěrům:
Dosažený cíl:prozkoumal trojúhelník a našel jeho pozoruhodné body.
Zadané úkoly byly vyřešeny:
1). Prostudovali jsme potřebnou literaturu;
2). Studovali jsme klasifikaci pozoruhodných bodů trojúhelníku;
3). Naučili jsme se, jak stavět nádherné trojúhelníkové body;
4). Shrnuli jsme prostudovaný materiál pro návrh brožury.
Potvrdila se hypotéza, že schopnost najít pozoruhodné body trojúhelníku pomáhá při řešení konstrukčních problémů.
Práce důsledně nastiňuje techniky konstrukce pozoruhodných bodů trojúhelníku a poskytuje historické informace o geometrických konstrukcích.
Informace z této práce mohou být užitečné v hodinách geometrie v 7. ročníku. Brožura se může stát referenční knihou o geometrii na prezentované téma.
Bibliografie
Učebnice. L.S. Atanasyan „Geometrie třídy 7-9Mnemosyne, 2015.
Wikipediahttps://ru.wikipedia.org/wiki/Geometry#/media/File:Euclid%27s_postulates.png
Portal Scarlet Sails
Přední vzdělávací portál v Rusku http://cendomzn.ucoz.ru/index/0-15157
ČTYŘI VÝZNAMNÉ BODY
TROJÚHELNÍK
Geometrie
8. třída
Sacharová Natalia Ivanovna
Střední škola MBOU č. 28 v Simferopolu

- Průsečík střednic trojúhelníku
- Průsečík os trojúhelníku
- Průsečík výšek trojúhelníku
- Průsečík kolmých střednic trojúhelníku

Medián
Medián (BD) trojúhelníku je segment, který spojuje vrchol trojúhelníku se středem protější strany.

Mediány trojúhelníky se protínají v jednu chvíli (centrum gravitace trojúhelník) a jsou tímto bodem rozděleny v poměru 2:1, počítáno od vrcholu.

BISECTOR
Osa (AD) trojúhelníku je úsečkou vnitřního úhlu trojúhelníku. ∟
ŠPATNÝ = ∟CAD.

Každý bod úsečky nerozvinutého úhlu je od svých stran stejně vzdálený.
Zadní:
každý bod ležící uvnitř úhlu a stejně vzdálený od stran úhlu leží na něm osy.

Všechny úsečky trojúhelníky se protínají v jednom bodě - střed vepsaného
do trojúhelníku kruhy.
Poloměr kružnice (OM) je kolmice sestupující ze středu (TO) ke straně trojúhelníku

VÝŠKA
Výška (CD) trojúhelníku je kolmý segment nakreslený z vrcholu trojúhelníku na čáru obsahující opačnou stranu.

Výšky trojúhelníky (nebo jejich prodloužení) se protínají jeden směřovat.

STŘEDNÍ KODLICE
Kolmice (DF) nazývaná přímka kolmá ke straně trojúhelníku a dělící ji na polovinu.

Každý bod kolmice(m) k segmentu je stejně vzdálený od konců tohoto segmentu.
Zadní:
každý bod stejně vzdálený od konců segmentu leží na středovém bodu kolmý jemu.

Všechny odvěsny stran trojúhelníku se protínají v jednom bodě - střed popisovaného
poblíž trojúhelníku kruh
.
Poloměr kružnice opsané je vzdálenost od středu kružnice k libovolnému vrcholu trojúhelníku (OA).

Strana 177 č. 675 (kresba)

Domácí práce
S. 173 § 3 definice a věty str. 177 č. 675 (dokončit)
Baranova Elena
Tato práce zkoumá pozoruhodné body trojúhelníku, jejich vlastnosti a vzory, jako je devítibodová kružnice a Eulerova přímka. Je uvedeno historické pozadí objevu Eulerovy přímky a devítibodové kružnice. Je navržen praktický směr aplikace mého projektu.
Stažení:
Náhled:
Chcete-li používat náhledy prezentací, vytvořte si účet Google a přihlaste se k němu: https://accounts.google.com
Popisky snímků:
"NÁDHERNÉ BODY TROJÚHELNÍKU." (Aplikované a základní otázky matematiky) Elena Baranova 8. ročník, MKOU „SOŠ č. 20“ Poz. Novoizobilnyj, Dukhanina Tatyana Vasilievna, učitelka matematiky Městského vzdělávacího zařízení "Střední škola č. 20" Obec Novoizobilny 2013. Městská vládní vzdělávací instituce "Střední škola č. 20"
Cíl: studovat trojúhelník pro jeho pozoruhodné body, studovat jejich klasifikaci a vlastnosti. Cíle: 1. Prostudovat potřebnou literaturu 2. Prostudovat klasifikaci pozoruhodných bodů trojúhelníku 3.. Seznámit se s vlastnostmi pozoruhodných bodů trojúhelníku 4. Umět sestrojit pozoruhodné body trojúhelníku. 5. Prozkoumejte rozsah pozoruhodných bodů. Předmět studia - úsek matematika - geometrie Předmět studia - trojúhelník Relevance: rozšiřte si znalosti o trojúhelníku, vlastnostech jeho pozoruhodných bodů. Hypotéza: spojení mezi trojúhelníkem a přírodou
Průsečík odvěsnic je stejně vzdálený od vrcholů trojúhelníku a je středem kružnice opsané. Kružnice opsané trojúhelníkům, jejichž vrcholy jsou středy stran trojúhelníku a vrcholy trojúhelníku se protínají v jednom bodě, který se shoduje s průsečíkem odvěsnic.
Průsečík os průsečíku os trojúhelníku je stejně vzdálený od stran trojúhelníku. OM=OA=OB
Průsečík výšek Průsečík os trojúhelníku, jehož vrcholy jsou základnami výšek, se shoduje s průsečíkem výšek trojúhelníku.
Průsečík mediánů Mediány trojúhelníku se protínají v jednom bodě, který rozděluje každý medián v poměru 2:1, počítáno od vrcholu. Pokud je průsečík mediánů připojen k vrcholům, pak se trojúhelník rozdělí na tři trojúhelníky o stejné ploše. Důležitou vlastností průsečíku mediánů je skutečnost, že součet vektorů, jejichž začátek je průsečíkem mediánů, a konce jsou vrcholy trojúhelníků, je roven nule M1 N C B A m2 m3 M1 N C B A m2 m3 M1 N C B A m2 m3 M1 N C B A m2 m3
Torricelliho bod Poznámka: Torricelliho bod existuje, pokud jsou všechny úhly trojúhelníku menší než 120.
Kruh devíti bodů B1, A1, C1 – základny výšek; A2, B2, C2 – středy odpovídajících stran; A3, B3, C3 jsou středy segmentů AN, VN a CH.
Eulerova přímka Průsečík mediánů, průsečík výšek, střed kružnice o devíti bodech leží na jedné přímce, která se na počest matematika, který tento vzor určil, nazývá Eulerova přímka.
Něco málo z historie objevu pozoruhodných bodů V roce 1765 Euler zjistil, že středy stran trojúhelníku a základny jeho výšek leží na stejné kružnici. Nejúžasnější vlastností pozoruhodných bodů trojúhelníku je, že některé z nich jsou navzájem spojeny určitým poměrem. Průsečík střednic M, průsečík výšek H a střed opsané kružnice O leží na stejné přímce a bod M rozděluje úsečku OH tak, že vztah OM:OH = 1:2 je Tato věta byla prokázána Leonhardem Eulerem v roce 1765.
Spojení mezi geometrií a přírodou. V této poloze má potenciální energie nejmenší hodnotu a součet segmentů MA+MB+MC bude nejmenší a součet vektorů ležících na těchto segmentech se začátkem v Torricelliho bodě bude roven nule.
Závěry Dozvěděl jsem se, že kromě nádherných průsečíků výšek, mediánů, os a kolmiček, které znám, existují také nádherné body a čáry trojúhelníku. Znalosti získané na toto téma budu schopen využít ve své vzdělávací činnosti, samostatně aplikovat věty na určité problémy a aplikovat naučené věty v reálné situaci. Věřím, že používání úžasných bodů a čar trojúhelníku při učení matematiky je efektivní. Jejich znalost výrazně urychluje řešení mnoha úkolů. Navržený materiál lze využít jak v hodinách matematiky, tak v mimoškolních aktivitách pro žáky 5.–9.
Náhled:
Chcete-li použít náhled, vytvořte si účet Google a přihlaste se:








 středy stran Δ ABC; nechat H
1
a H - jejich ortocentra (obr. 65). Bod H 1 se shoduje se středem O kružnice opsané Δ ABC. Dokažme, že Δ
středy stran Δ ABC; nechat H
1
a H - jejich ortocentra (obr. 65). Bod H 1 se shoduje se středem O kružnice opsané Δ ABC. Dokažme, že Δ