Рационална функция е дроб от формата , чиито числител и знаменател са полиноми или произведения на полиноми.
Пример 1. Стъпка 2.
.
Умножаваме неопределените коефициенти по полиноми, които не са в тази отделна дроб, но които са в други получени дроби:
Отваряме скобите и приравняваме числителя на оригиналния интегранд към получения израз:
В двете страни на равенството търсим членове с еднакви степени на x и съставяме система от уравнения от тях:
.
Съкращаваме всички х-ове и получаваме еквивалентна система от уравнения:
.
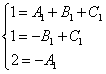По този начин, окончателното разширяване на интегранта в сбор от прости дроби е:
.
Пример 2. Стъпка 2.На стъпка 1 получихме следното разлагане на оригиналната дроб в сумата от прости дроби с неопределени коефициенти в числителите:
.
Сега започваме да търсим несигурни коефициенти. За да направим това, ние приравняваме числителя на първоначалната дроб във функционалния израз на числителя на израза, получен след намаляване на сумата от дроби до общ знаменател:
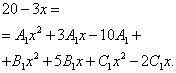
Сега трябва да създадете и решите система от уравнения. За да направим това, приравняваме коефициентите на променливата към съответната степен в числителя на оригиналния израз на функцията и подобни коефициенти в израза, получен в предишната стъпка:
Решаваме получената система:
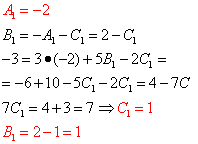
И така, от тук
.
Пример 3. Стъпка 2.На стъпка 1 получихме следното разлагане на оригиналната дроб в сумата от прости дроби с неопределени коефициенти в числителите:
Започваме да търсим несигурни коефициенти. За да направим това, ние приравняваме числителя на първоначалната дроб във функционалния израз към числителя на израза, получен след намаляване на сумата от дроби до общ знаменател:
Както в предишните примери, съставяме система от уравнения:
Редуцираме х-овете и получаваме еквивалентна система от уравнения:
Решавайки системата, получаваме следните стойности на несигурните коефициенти:
Получаваме окончателното разлагане на интегранта в сумата от прости дроби:
.
Пример 4. Стъпка 2.На стъпка 1 получихме следното разлагане на оригиналната дроб в сумата от прости дроби с неопределени коефициенти в числителите:
.
Вече знаем от предишни примери как да приравним числителя на първоначалната дроб с израза в числителя, получен след разлагането на дробта на сбора от прости дроби и привеждането на тази сума към общ знаменател. Следователно, само за целите на контрола, представяме получената система от уравнения:
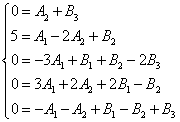
Решавайки системата, получаваме следните стойности на несигурните коефициенти:
Получаваме окончателното разлагане на интегранта в сумата от прости дроби:
Пример 5. Стъпка 2.На стъпка 1 получихме следното разлагане на оригиналната дроб в сумата от прости дроби с неопределени коефициенти в числителите:
.
Ние независимо намаляваме тази сума до общ знаменател, приравнявайки числителя на този израз към числителя на оригиналната дроб. Резултатът трябва да бъде следната система от уравнения:
Решавайки системата, получаваме следните стойности на несигурните коефициенти:
.
Получаваме окончателното разлагане на интегранта в сумата от прости дроби:
.
Пример 6. Стъпка 2.На стъпка 1 получихме следното разлагане на оригиналната дроб в сумата от прости дроби с неопределени коефициенти в числителите:
Извършваме същите действия с тази сума, както в предишните примери. Резултатът трябва да бъде следната система от уравнения:
Решавайки системата, получаваме следните стойности на несигурните коефициенти:
.
Получаваме окончателното разлагане на интегранта в сумата от прости дроби:
.
Пример 7. Стъпка 2.На стъпка 1 получихме следното разлагане на оригиналната дроб в сумата от прости дроби с неопределени коефициенти в числителите:
.
След определени действия с получената сума трябва да се получи следната система от уравнения:
Решавайки системата, получаваме следните стойности на несигурните коефициенти:
Получаваме окончателното разлагане на интегранта в сумата от прости дроби:
.
Пример 8. Стъпка 2.На стъпка 1 получихме следното разлагане на оригиналната дроб в сумата от прости дроби с неопределени коефициенти в числителите:
.
Нека направим някои промени в действията, които вече са автоматизирани, за да получим система от уравнения. Има изкуствена техника, която в някои случаи помага да се избегнат ненужни изчисления. Привеждайки сумата от дроби към общ знаменател, получаваме и приравнявайки числителя на този израз към числителя на оригиналната дроб, получаваме.
Тук предоставяме подробни решения на три примера за интегриране на следните рационални дроби:
,
,
.
Пример 1
Изчислете интеграла:
.
Решение
Тук под знака за интеграл има рационална функция, тъй като интеграндът е част от полиноми. Степен на полинома на знаменателя ( 3 ) е по-малка от степента на полинома на числителя ( 4 ). Следователно, първо трябва да изберете цялата част от фракцията.
1.
Нека изберем цялата част от дробта. Разделете x 4
от x 3 - 6 x 2 + 11 x - 6:
Оттук
.
2.
Нека разложим на множители знаменателя на дробта. За да направите това, трябва да решите кубичното уравнение:
.
6
1, 2, 3, 6, -1, -2, -3, -6
.
Нека заместим x = 1
:
.
1
. Разделете на x - 1
:
Оттук
.
Решаване на квадратно уравнение.
.
Корените на уравнението са: , .
Тогава
.
3.
Нека разделим дробта на най-простата й форма.
.
Така открихме:
.
Да се интегрираме.
Отговор
Пример 2
Изчислете интеграла:
.
Решение
Тук числителят на дробта е полином от нулева степен ( 1 = х 0). Знаменателят е полином от трета степен. Тъй като 0 < 3 , тогава дробта е правилна. Нека го разделим на прости дроби.
1.
Нека разложим на множители знаменателя на дробта. За да направите това, трябва да решите уравнение от трета степен:
.
Да приемем, че има поне един цял корен. Тогава то е делител на числото 3
(член без x). Тоест, целият корен може да бъде едно от числата:
1, 3, -1, -3
.
Нека заместим x = 1
:
.
И така, намерихме един корен x = 1
. Разделете x 3 + 2 х - 3на х - 1
:
Така,
.
Решаване на квадратното уравнение:
х 2 + x + 3 = 0.
Намерете дискриминанта: D = 1 2 - 4 3 = -11. Тъй като Д< 0
, тогава уравнението няма реални корени. Така получихме факторизирането на знаменателя:
.
2.
.
(x - 1)(x 2 + x + 3):
(2.1)
.
Нека заместим x = 1
. Тогава х - 1 = 0
,
.
Да заместим (2.1)
x = 0
:
1 = 3 A - C;
.
Нека се приравним към (2.1)
коефициенти за х 2
:
;
0 = A + B;
.
.
3.
Да се интегрираме.
(2.2)
.
За да изчислим втория интеграл, избираме производната на знаменателя в числителя и редуцираме знаменателя до сбора от квадрати.
;
;
.
Изчислете I 2
.
.
Тъй като уравнението x 2 + x + 3 = 0няма реални корени, тогава x 2 + x + 3 > 0. Следователно знакът за модул може да бъде пропуснат.
Ние доставяме до (2.2)
:
.
Отговор
Пример 3
Изчислете интеграла:
.
Решение
Тук под знака за интеграл има част от полиномите. Следователно интегрантът е рационална функция. Степента на полинома в числителя е равна на 3 . Степента на полинома на знаменателя на дробта е равна на 4 . Тъй като 3 < 4 , тогава дробта е правилна. Следователно може да се разложи на прости дроби. Но за да направите това, трябва да разложите знаменателя на множители.
1.
Нека разложим на множители знаменателя на дробта. За да направите това, трябва да решите уравнението от четвърта степен:
.
Да приемем, че има поне един цял корен. Тогава то е делител на числото 2
(член без x). Тоест, целият корен може да бъде едно от числата:
1, 2, -1, -2
.
Нека заместим x = -1
:
.
И така, намерихме един корен x = -1
. Разделете на x - (-1) = x + 1:
Така,
.
Сега трябва да решим уравнение от трета степен:
.
Ако приемем, че това уравнение има корен от цяло число, тогава то е делител на числото 2
(член без x). Тоест, целият корен може да бъде едно от числата:
1, 2, -1, -2
.
Нека заместим x = -1
:
.
И така, намерихме друг корен x = -1
. Би било възможно, както в предишния случай, да разделим полинома на , но ще групираме условията:
.
Тъй като уравнението x 2 + 2 = 0
няма реални корени, тогава получаваме факторизацията на знаменателя:
.
2.
Нека разбием дробта в най-простата й форма. Търсим разширение във формата:
.
Отърваваме се от знаменателя на дробта, умножаваме по (x + 1) 2 (x 2 + 2):
(3.1)
.
Нека заместим x = -1
. Тогава x + 1 = 0
,
.
Нека разграничим (3.1)
:
;
.
Нека заместим x = -1
и вземете предвид, че x + 1 = 0
:
;
;
.
Да заместим (3.1)
x = 0
:
0 = 2 A + 2 B + D;
.
Нека се приравним към (3.1)
коефициенти за х 3
:
;
1 = B + C;
.
И така, намерихме разлагането на прости дроби:
.
3.
Да се интегрираме.
.
2.,
5.
,
3.
,
6.
.
В интеграли 1-3 ас u
приемам 
. След това н-многократно прилагане на формула (19) стигаме до един от табличните интеграли
,
,
.
В интеграли 4-6, когато диференцирате, опростете трансценденталния фактор 
,
или 
, което трябва да се приема като u.
Изчислете следните интеграли.
Пример 7.
Пример 8. 
Намаляване на интегралите до себе си
Ако подинтегралната функция 
има формата:
,
,
и така нататък,
тогава след интегриране два пъти по части получаваме израз, съдържащ първоначалния интеграл 
:
,
Където 
- някаква константа.
Решаване на полученото уравнение за 
, получаваме формула за изчисляване на първоначалния интеграл:
.
Този случай на прилагане на метода на интегриране по части се нарича " привеждане на интеграла към себе си».
Пример 9.Изчислете интеграл
.
От дясната страна е оригиналният интеграл 
. Премествайки го вляво, получаваме:
.
Пример 10.Изчислете интеграл
.
4.5. Интегриране на най-простите правилни рационални дроби
Определение.Най-простите правилни дроби аз , II И III видове Следните дроби се наричат:
аз.
;
II.
;
(
- положително цяло число);
III.
; (корените на знаменателя са сложни, тоест: 
.
Нека разгледаме интеграли от прости дроби.
аз.
;
(20)
II. ; (21)
III.
;
Трансформираме числителя на дробта по такъв начин, че да изолираме члена в числителя 
, равно на производната на знаменателя.
Нека разгледаме първия от двата получени интеграла и да направим промяна в него:
Във втория интеграл добавяме знаменателя към перфектен квадрат:
И накрая, интегралът на дроб от трети тип е равен на:
=
+
.
(22)
Така интегралът на най-простите дроби от тип I се изразява чрез логаритми, тип II - чрез рационални функции, тип III - чрез логаритми и арктангенси.
4.6.Интегриране на дробно-рационални функции
Един от класовете функции, които имат интеграл, изразен чрез елементарни функции, е класът на алгебрични рационални функции, тоест функции, произтичащи от краен брой алгебрични операции върху аргумент.
Всяка рационална функция 
може да се представи като отношение на два полинома 
И 
:
.
(23)
Ще приемем, че полиномите нямат общи корени.
Извиква се дроб от формата (23). правилно, ако степента на числителя е по-малка от степента на знаменателя, т.е. м< н. В противен случай - грешно.
Ако дробта е неправилна, то като разделим числителя на знаменателя (съгласно правилото за деление на полиноми), представяме дробта като сбор от полином и правилна дроб:
,
(24)
Където 
- полином, 
- правилна дроб и степента на полинома 
- не по-висока от степен ( н-1).
Пример. 
Тъй като интегрирането на полином се свежда до сумата от таблични интеграли на степенна функция, основната трудност при интегрирането на рационални дроби се крие в интегрирането на правилните рационални дроби.
В алгебрата е доказано, че всяка правилна дроб 
се разлага на сумата от горното протозоидроби, чиято форма се определя от корените на знаменателя 
.
Нека разгледаме три специални случая. Тук и по-нататък ще приемем, че коеф 
на най-високата степен на знаменателя 
равно на едно 
=1, т.енамален полином
.
Случай 1.Корените на знаменателя, тоест корените 
уравнения 
=0, са валидни и различни. След това представяме знаменателя като произведение на линейни множители:
и правилната дроб се разлага на най-простите дроби от I-gotype:
,
(26)
Където 
– някои постоянни числа, които се намират по метода на неопределените коефициенти.
За да направите това ви трябва:
1. Приведете дясната страна на разширението (26) към общ знаменател.
2. Приравнете коефициентите на еднакви степени на еднакви полиноми в числителя на лявата и дясната страна. Получаваме система от линейни уравнения за определяне 
.
3. Решете получената система и намерете неопределените коефициенти 
.
Тогава интегралът на дробно-рационалната функция (26) ще бъде равен на сумата от интегралите на най-простите дроби от I-тип, изчислени по формула (20).
Пример.Изчислете интеграл 
.
Решение.Нека разложим знаменателя на множители, използвайки теоремата на Виета:
След това функцията интегранд се разлага на сбор от прости дроби:
.
х:
Нека напишем система от три уравнения, които да намерим 
хот лявата и дясната страна:
.
Нека посочим по-прост начин за намиране на несигурни коефициенти, наречен метод на частична стойност.
Приемайки равенство (27) 
получаваме 
, където 
. Вярвайки 
получаваме 
. Накрая, вярвайки 
получаваме 
.
.
Случай 2.Корен на знаменателя 
са валидни, но сред тях има множество (равни) корени. След това представяме знаменателя като произведение на линейни множители, включени в произведението до степента, в която кратността на съответния корен е:
Където 
.
Правилна дроб 
ще се разложи сумата от дроби от тип I и II. нека например 
- корен от знаменателя на кратността к, и всички останали ( н-
к) корените са различни.
Тогава разширението ще изглежда така:
По същия начин, ако има други множество корени. За некратни корени разширението (28) включва най-простите дроби от първия тип.
Пример.Изчислете интеграл 
.
Решение.Нека си представим дробта като сбор от най-простите дроби от първи и втори вид с неопределени коефициенти:
.
Нека приведем дясната страна към общ знаменател и приравним полиномите в числителите на лявата и дясната страна:
От дясната страна представяме подобни със същите степени х:
Нека напишем система от четири уравнения, които да намерим 
И 
. За да направим това, приравняваме коефициентите при еднакви степени хот лявата и дясната страна
.
Случай 3.Сред корените на знаменателя 
има сложни единични корени. Тоест, разширяването на знаменателя включва фактори от втора степен 
, които не се разлагат на реални линейни множители и не се повтарят.
Тогава, при разлагането на дроб, всеки такъв фактор ще съответства на най-простата дроб от тип III. Линейните множители съответстват на най-простите дроби от тип I и II.
Пример.Изчислете интеграл 
.
Решение.
.
.
.
Преди това обсъдихме общи методи за интеграция. В този и следващите параграфи ще говорим за интегрирането на специфични класове функции с помощта на обсъжданите техники.
Интегриране на най-простите рационални функции
Нека разгледаме интеграл от формата \textstyle(\int R(x)\,dx), където y=R(x) е рационална функция. Всеки рационален израз R(x) може да бъде представен във формата \frac(P(x))(Q(x)), където P(x) и Q(x) са полиноми. Ако тази дроб е неправилна, тоест ако степента на числителя е по-голяма или равна на степента на знаменателя, тогава тя може да бъде представена като сбор от полином (цяла част) и правилна дроб. Следователно е достатъчно да разгледаме интегрирането на правилните дроби.
Нека покажем, че интегрирането на такива дроби се свежда до интегрирането прости дроби, т.е. изрази от формата:
\mathsf(1))~\frac(A)(x-a);\quad \mathsf(2))~\frac(A)((x-a)^n);\quad \mathsf(3))~ \frac( Ax+B)(x^2+px+q);\quad \mathsf(4))~\frac(Ax+B)((x^2+px+q)^n).
Където A,\,B,\,a,\,p,\,qса реални числа, а квадратният трином x^2+px+q няма реални корени. Изрази от тип 1) и 2) се наричат дроби от 1-ви род, а изрази от тип 3) и 4) се наричат дроби от 2-ри род.
Интегралите на дроби от 1-ви род се изчисляват директно
\begin(aligned)\mathsf(1))&~\int\frac(A)(x-a)\,dx= A\ln|x-a|+C;\\ \mathsf(2))&~ \int\frac (A)((x-a)^n)\,dx= A\int(x-a)^(-n)\,dx= A\,\frac((x-a)^(-n+1))(-n+ 1 )+C~(n=2,3,4,\lточки). \край (подравнено)
Нека разгледаме изчисляването на интеграли на дроби от 2-ри вид: \mathsf(3))~ \int\frac(Ax+B)(x^2+px+q)\,dx\,.
Първо отбелязваме, че
\int\frac(dt)(t^2+a^2)= \frac(1)(a)\име на оператор(arctg)\frac(t)(a)+C,\qquad \int\frac(t\ ,dt)(t^2+a^2)= \frac(1)(2)\ln(t^2+a^2)+C.
За да намалим изчислението на интеграл 3) до тези два интеграла, трансформираме квадратния трином x^2+px+q, като отделяме пълния квадрат от него:
x^2+px+q= (\left(x+\frac(p)(2)\right)\^2+ \left(q-\frac{p^2}{4}\right)\!. !}
Тъй като по предположение този тричлен няма реални корени, тогава q-\frac(p^2)(4)>0и можем да сложим q-\frac(p^2)(4)=a^2. Заместване x+\frac(p)(2)=t,~ dx=dtпреобразува интеграл 3) в линейна комбинация от посочените два интеграла:
\begin(aligned)\int\frac(Ax+B)(x^2+px+q)\,dx&= \int\frac(A\!\left(t-\frac(p)(2)\right) )+B)(t^2+a^2)\,dt= A\int\frac(t\,dt)(t^2+a^2)+ \left(B-\frac(Ap)(2 )\right)\!\int\frac(dt)(t^2+a^2)=\\ &=\frac(A)(2)\ln(t^2+a^2)+ \frac( 1)(a)\!\left(B-\frac(Ap)(2)\right)\!\ \operatorname(arctg)\frac(t)(a)+C. \край (подравнено)
В крайния отговор трябва само да замените (t) с x+\frac(p)(2) и (a) с \sqrt(q-\frac(p^2)(4)). Тъй като t^2+a^2=x^2+px+q, тогава
\int\frac(Ax+B)(x^2+px+q)\,dx= \frac(A)(2)\ln(x^2+px+q)+ \frac(B-\dfrac( Ap)(2))(\sqrt(q-\dfrac(p^2)(4))) \operatorname(arctg)\frac(x+\dfrac(p)(2))(\sqrt(q-\dfrac (p^2)(4)))+C.
Разгледайте случая \mathsf(4))~ \int\frac(Ax+B)((x^2+px+q)^n)\,dx.
Както в предишния случай, нека зададем x+\frac(p)(2)=t. Получаваме:
\int\frac(Ax+B)((x^2+px+q)^n)\,dx= A\int\frac(t\,dt)((t^2+a^2)^n) + \left(B-\frac(Ap)(2)\right)\! \int\frac(dt)((t^2+a^2)^n)\,.
Първият член се изчислява, както следва:
A\int\frac(t\,dt)((t^2+a^2)^n)= \frac(A)(2)\int(t^2+a^2)^(-n)\ ,d(t^2+a^2)= \frac(A)(2)\frac((t^2+a^2)^(-n+1))(-n+1)= \frac( A)(2(1-n)(t^2+a^2)^(n-1))\,.
Вторият интеграл се изчислява с помощта на рекурентна формула.
Пример 1.Нека изчислим \int\frac(3x+2)(x^2+2x+3)\,dx.
Решение.Ние имаме: x^2+2x+3=(x+1)^2+2. Нека поставим x+1=t. Тогава dx=dt и 3x+2=3(t-1)+2=3t-1и следователно
\begin(aligned)\int\frac(3x+2)(x^2+2x+3)\,dx&= \int\frac(3t-1)(t^2+2)\,dt= \frac( 3)(2)\int\frac(2t\,dt)(t^2+2)- \int\frac(dt)(t^2+(\sqrt(2))^2)=\\ &= \frac(3)(2)\ln(t^2+2)- \frac(1)(\sqrt(2))\име на оператор(arctg)\frac(t)(\sqrt(2))+C= \\ &=\frac(3)(2)\ln(x^2+2x+3)- \frac(1)(\sqrt(2))\име на оператор(arctg)\frac(x+1)(\ sqrt(2))+C. \край (подравнено)
Пример 2.Нека изчислим \int\frac(x+2)((x^2+6x+10)^2)\,dx.
Решение.Ние имаме: x^2+6x+10=(x+3)^2+1. Нека въведем нова променлива, като зададем x+3=t. Тогава dt=dx и x+2=t-1. Заменяйки променливата под интегралния знак, получаваме:
\begin(aligned)\int\frac(x+2)((x^2+6x+10)^2)\,dx&= \int\frac(t-1)((t^2+1)^2 )\,dt= \frac(1)(2)\int\frac(2t\,dt)((t^2+1)^2)-\int\frac(dt)((t^2+1) ^2)=\\ &=-\frac(1)(2(t^2+1))- \int\frac(dt)((t^2+1)^2)\,. \край (подравнено))
Да сложим I_2=\int\frac(dt)((t^2+1)^2). Ние имаме:
I_2=\frac(1)(2)I_1+\frac(1)(2)\frac(t)(t^2+1), Но I_1=\int\frac(dt)(t^2+1)= \operatorname(arctg)tПо този начин, I_2= \frac(1)(2)\operatorname(arctg)t+ \frac(t)(2(t^2+1)).
Накрая получаваме:
\begin(aligned)\int\frac(x+2)((x^2+6x+10)^2)\,dx&=-\frac(1)(2(t^2+1))-\frac (1)(2)\име на оператор(arctg)t-\frac(t)(2(t^2+1))=\\ &=-\frac(1)(2(x^2+6x+10) )- \frac(1)(2)\име на оператор(arctg)(x+3)- \frac(x+3)(2(x^2+6x+10))+C=\\ &=\frac( -x-4)(2(x^2+6x+10))-\frac(1)(2)\operatorname(arctg)(x+3)+C \end(aligned)
Интегриране на правилни дроби
Помислете за правилна дроб R(x)=\frac(P(x))(Q(x)), където Q(x) е полином от степен n. Без загуба на общност можем да приемем, че водещият коефициент в Q(x) е равен на 1. В курс по алгебра е доказано, че такъв полином с реални коефициенти може да бъде разложен на множители от първа и втора степен с реални коефициенти :
Q(x)= (x-x_1)^(\alpha)\ldots (x-x_k)^(\beta) (x^2+p\,x+q)^(\gamma)\ldots (x^2 +r\,x+s)^(\delta).
където x_1,\ldots,x_k са реалните корени на полинома Q(x) и квадратните триноми нямат реални корени. Може да се докаже, че тогава R(x) е представено като сума от прости дроби във формата 1) -4):
\begin(aligned)R(x)=&\frac(P(x))(Q(x))= \frac(A_1)((x-x_1)^(\alpha))+ \frac(A_2)( (x-x_1)^(\alpha-1))+\ldots+ \frac(A_(\alpha))(x-x_1)\,+\\ &+\,\ldots+ \frac(B_1)((x- x_k)^(\beta))+ \frac(B_2)((x-x_k)^(\beta-1))+\ldots+ \frac(B_(\beta))(x-x_k)+ \frac(M_1x+ N_1)((x^2+p\,x+q)^(\gamma))\,+\\ &+\,\ldots+ \frac(M_(\gamma)+ N_(\gamma))(x^ 2+ p\,x+s)+ \frac(E_1x+F_1)((x^2+rx+s)^(\delta))+\ldots+ \frac(E_(\delta)x+F_(\delta ))(x^2+rx+s)\, \end(подравнено)
където показателите на знаменателите последователно намаляват от \alpha до 1, ..., от \beta до 1, от \gamma до 1, ..., от \delta до 1 и A_1,\lточки,F_(\delta)- несигурни коефициенти. За да се намерят тези коефициенти, е необходимо да се отървете от знаменателите и след като сте получили равенството на два полинома, използвайте метода на неопределените коефициенти.
Друг начин за определяне на коефициентите A_1,\ldots, A_(\alpha), \ldots, F_(\delta)се основава на заместване на стойностите на променливата x. Замествайки произволно число вместо x в равенството, получено от равенство (1) след премахване на знаменателите, стигаме до линейно уравнение за търсените коефициенти. Като заместим необходимия брой такива частични стойности на променливата, получаваме система от уравнения за намиране на коефициентите. Най-удобно е да изберете корените на знаменателя (реални и комплексни) като частни стойности на променливата. В този случай почти всички членове от дясната страна на равенството (което означава равенство на два полинома) изчезват, което улеснява намирането на останалите коефициенти. Когато замествате комплексни стойности, имайте предвид, че две комплексни числа са равни тогава и само ако техните реална и имагинерна част са равни съответно. Следователно от всяко равенство, съдържащо комплексни числа, се получават две уравнения.
След намирането на неопределените коефициенти остава да се изчислят интегралите на получените най-прости дроби. Тъй като при интегрирането на най-простите дроби, както видяхме, се получават само рационални функции, арктангенси и логаритми, тогава интегралът на всяка рационална функция се изразява чрез рационална функция, арктангенси и логаритми.
Пример 3.Нека изчислим интеграла на правилна рационална дроб \int\frac(6x+1)(x^2+2x-3)\,dx.
Решение.Нека факторизираме знаменателя на интегранта:
x^2+2x-3=(x-1)(x+3).
Нека напишем интегранта и го представим като сбор от прости дроби:
\frac(6x+1)(x^2+2x-3)= \frac(A)(x-1)+\frac(B)(B+3)\,.
Освобождавайки се от знаменателите в това равенство, получаваме:
6x+1=A\cdot (x+3)+B\cdot (x-1)\,.
За да намерим коефициентите, ще използваме метода на заместване на частични стойности. За да намерим коефициента A, нека зададем x=1. Тогава от равенство (2) получаваме 7=4A, откъдето A=7/4. За да намерим коефициента B, нека зададем x=-3. Тогава от равенство (2) получаваме -17=-4B, откъдето B=17/4.
Така, \frac(6x+1)(x^2+2x-3)= \frac(7)(4)\cdot\frac(1)(x-1)+ \frac(17)(4)\cdot\frac (1)(x+3). означава,
\int\frac(6x+1)(x^2+2x-3)\,dx= \frac(7)(4)\int\frac(dx)(x-1)+ \frac(17)(4 )\int\frac(dx)(x+3)= \frac(7)(4)\ln|x-1|+ \frac(17)(4)\ln|x+3|+C.
Пример 4.Нека изчислим \int\frac(x^4+2x^2+8x+5)((x^2+2)(x-1)^2(x+2))\,dx.
Решение.Нека напишем интегранта и го представим като сбор от прости дроби. Знаменателят съдържа множител x^2+2, който няма реални корени; той съответства на дроб от 2-ри род: \frac(Ax+B)(x^2+2)множителят (x-1)^2 съответства на сумата от две дроби от 1-ви вид: \frac(C)((x-1)^2)+ \frac(D)(x-1); накрая, факторът x+2 съответства на една дроб от 1-ви вид \frac(E)(x+2) . Така представяме функцията интегранд като сбор от четири дроби:
\frac(x^4+2x^2+8x+5)((x^2+2)(x-1)^2(x+2))= \frac(Ax+B)(x^2+2 )+ \frac(C)((x-1)^2)+ \frac(D)(x-1)+ \frac(E)(x+2)\,.
Нека се освободим от знаменателите в това равенство. Получаваме:
\begin(aligned) x^4+2x^2+8x+5&= (Ax+B)(x-1)^2(x+2)+ C(x^2+2)(x+2)\, +\\ &\фантом(=)+ D(x^2+2)(x-1)(x+2)+ E(x^2+2)(x-1)^2.\end(подравнено)
Знаменателят на интегранта има два реални корена: x=1 и x=-2. При заместване на стойността x=1 в равенство (4) получаваме 16=9C, от което намираме C=16/9. При заместване на x=-2 получаваме 13=54E и съответно дефинираме E=13/54. Заместването на стойността x=i\,\sqrt(2) (коренът на полинома x^2+2 ) ни позволява да стигнем до равенството
4-4+8\,i\,\sqrt(2)+5= (A\,i\,\sqrt(2)+B)\cdot (i\,\sqrt(2)-1)^2\ cdot (i\,\sqrt(2)+2).
Трансформира се във формата:
(10A+2B)+(2A-5B)\sqrt(2)\,i= 5+8\sqrt(2)\,i, от където 10A+2B=5, и (2A-5B)\sqrt(2)=8\sqrt(2).
Решаване на система от две уравнения с две променливи \begin(cases)10A+2B=5,\\ 2A-5B=8,\end(cases)намираме: A=\frac(41)(54),~ B=-\frac(35)(27).
Остава да се определи стойността на коефициента D. За да направим това, в равенство (4) отваряме скобите, представяме подобни членове и след това сравняваме коефициентите за x^4. Получаваме:
A+D+E=1, което е D=0.
Нека заместим намерените стойности на коефициентите в равенство (3):
\frac(x^4+2x^2+8x+5)((x^2+2)(x-1)^2(x+2))= \frac(\drac(41)(54)\, x- \dfrac(35)(27))(x^2+2)+ \frac(16)(9)\frac(1)((x-1)^2)+ \frac(13)(54) \frac(1)(x+2)\,
и след това преминете към интеграция:
\begin(aligned)\int\frac(x^4+2x^2+8x+5)((x^2+2)(x-1)^2(x+2))\,dx&= \frac( 41)(54)\int\frac(x\,dx)(x^2+2)- \frac(35)(27)\int\frac(dx)(x^2+2)+ \frac(16 )(9) \int\frac(dx)((x-1)^2)+ \frac(13)(54)\int\frac(dx)(x+2)=\\ &=\frac(41) )(108)\ln(x^2+2)- \frac(35)(27\sqrt(2))\име на оператор(arctg)\frac(x)(\sqrt(2))- \frac(16) (9(x-1))+ \frac(13)(54) \ln|x+2|+C.\end(подравнено)
Интегриране на неправилни дроби
Да предположим, че трябва да интегрираме функцията y=\frac(f(x))(g(x)), където f(x) и g(x) са полиноми, а степента на полинома f(x) е по-голяма или равна на степента на полинома g(x) . В този случай, първо, трябва да изберете цялата част от неправилната фракция \frac(f(x))(g(x)), т.е. представя го във формата
\frac(f(x))(g(x))=s(x)+ \frac(r(x))(g(x))\,
където s(x) е полином със степен, равна на разликата между степените на полиномите f(x) и g(x), и \frac(r(x))(g(x))- правилна дроб.
Тогава имаме \int\frac(f(x))(g(x))\,dx= \int s(x)\,dx+ \int\frac(r(x))(g(x))\,dx\, ..
Пример 5.Нека изчислим интеграла на неправилната дроб \int\frac(x^4-4x^3+x^2+16x-11)((x-1)(x+2)(x-3))\,dx.
Решение.Ние имаме:
\begin(aligned)g(x)&=(x-1)(x+2)(x-3)= x^3-2x^2-5x+6,\\ f(x)&=x^4 -4x^3+x^2+16x-11. \край (подравнено)
За да изолирате цялата част, разделете f(x) на g(x): \frac(f(x))(g(x))= x-2+\frac(2x^2+1)(x^3-2x^2-5x+6)\,.
означава, \int\frac(x^4-4x^3+x^2+16x-11)((x-1)(x+2)(x-3))\,dx= \int(x-2)dx+ \int\frac(2x^2+1)((x-1)(x+2)(x-3))\,dx
Ние имаме: \int(x-2)dx=\frac(x^2)(2)-2x+C.
За изчисляване на интеграла \int\frac(2x^2+1)((x-1)(x+2)(x-3))\,dxИзползва се методът на неопределените коефициенти, както по-горе. След изчисленията, които оставяме на читателя, получаваме.
Интегриране на рационални функции Дробна - рационална функция Най-простите рационални дроби Разлагане на рационална дроб на прости дроби Интегриране на прости дроби Общо правило за интегриране на рационални дроби
полином от степен n. Дробно-рационална функция Дробно-рационална функция е функция, равна на съотношението на два полинома: Рационална дроб се нарича правилна, ако степента на числителя е по-малка от степента на знаменателя, т.е. m< n , в противном случае дробь называется неправильной. многочлен степени m Всякую неправильную рациональную дробь можно, путем деления числителя на знаменатель, представить в виде суммы многочлена L(x) и правильной рациональной дроби:)()()(x. Q x. P xf n m)()()(x. Q x. R x. L x. Q x. P
Дробна - рационална функция Редуцирайте неправилна дроб до правилната форма: 2 95 4 x xx 95 4 xx 2 x 3 x 34 2 xx 952 3 xx 2 2 x 23 42 xx 954 2 xx x 4 xx 84 2 93 x 3 63 x 15 2 95 4 x xx 342 23 xxx 2 15 x
Най-прости рационални дроби Правилни рационални дроби от вида: Те се наричат най-прости рационални дроби от типове. брадва A); 2(Nkk ax A k)04(2 2 qp qpxx NMx); 2; 04(2 2 Nkkqp qpxx NMx k V V,
Разлагане на рационална дроб на прости дроби Теорема: Всяка правилна рационална дроб, чийто знаменател е факторизиран: може да бъде представена освен това по уникален начин под формата на сбор от прости дроби: s k qxpxxxxxx. Q)()()(22 2 11 2 21)()(x. Q x. P 1 xx A k k xx B)()(2 2 2 1 11 2 qxpx DCx 2 22 22 2 11)(qxpx Nx. M s ss qxpx Nx)
Разлагане на рационална дроб на прости дроби Нека обясним формулировката на теоремата, като използваме следните примери: За намиране на несигурните коефициенти A, B, C, D... се използват два метода: методът на сравняване на коефициентите и методът на частични стойности на променлива. Нека разгледаме първия метод с пример. 3 2)3)(2(4 xx x 2 x A 3 3 2 21)3()3(3 x B x B 1 2 x DCx 22 22 2 11)1(1 xx Nx. M)1(3 22 3 xx x 2 21 x A 22 2)1)(4(987 xxx xx 4 x
Разлагане на рационална дроб на прости дроби. Представете дробта като сбор от прости дроби: Нека приведем най-простите дроби към общ знаменател. Приравнете числителите на получената и първоначалната дроби. Приравнете коефициентите при еднакви степени x)52)(1( 332 2 2 xxx xx 1 x A 52 2 xx CBx )52)(1()1)(()52(2 2 xxx x. CBxxx. A 33252 222 xx. CBx. Cx. Bx. AAx. Ax 35 32 2 0 1 2 CAx BAx 2 3 1 C B A 52 23 1 1 2 xx x x
Интегриране на най-простите дроби Нека намерим интегралите на най-простите рационални дроби: Нека разгледаме интегрирането на дроби от тип 3, използвайки пример. dx ax A k dx qpxx NMx 2 ax axd A)(Cax. Aln)(axdax. A k C k ax. A k
Интегриране на прости дробиdx xx x 102 13 2 dx xx x 9)12(13 2 dx x x 9)1(13 2 dtdx tx tx 1 1 dt t t 9 1)1(3 2 dt t t 9 23 2 9 322 t dtt 9 9 2 3 2 2 t td 33 2 t arctgt 33 2 9 ln 2 32 C x arctgxx 3 1 3 2 102 ln.
Интегриране на прости дроби Интеграл от този тип, използващ заместване: се редуцира до сумата от два интеграла: Първият интеграл се изчислява чрез въвеждане на t под диференциалния знак. Вторият интеграл се изчислява с помощта на рекурентната формула: dx qpxx NMx k 2 V t p x 2 kk при dt N при dtt M 22122 1221222))(1(222 321 kkkk atk t k k aat dt
Интегриране на прости дроби a = 1; k = 3 323)1(t dt tarctg t dt 1 21)1)(12(2222 322 1 21222 t t t dt)1(22 1 2 t t tarctg 2223)1)(13(2232 332 t t C t t tarctg 222)1 (4)1(
Общо правило за интегриране на рационални дроби Ако дробта е неправилна, тогава я представете като сбор от полином и правилна дроб. След като факторизирате знаменателя на правилна рационална дроб, представете го като сума от прости дроби с неопределени коефициенти по метода на сравняване на коефициентите или по метода на частичните стойности на променлива. Интегрирайте полинома и получената сума от прости дроби.
Пример Нека поставим дробта в правилната форма. dx xxx 23 35 2 442 35 xxxxxx 23 2 2 x 345 2 xxx 442 34 xxx x 2 234 242 xxx 4425 23 xxx xxx 23 35 2 442 xxx xx xx 23 2 2 2 48 52 5 xxx 5105 23 48 2 x х
Пример Нека разложим на множители знаменателя на правилна дроб. Нека представим дробта като сбор от прости дроби. Да намерим неопределените коефициенти, като използваме метода на частичните стойности на променливата xxx xx 23 2 2 48 2 2)1(48 xx xx 2 )1(1 x C x B x A 2 2)1 ()1(xx Cxx. Bxx. A 48)1()1(22 xx. Cxx. Bxx. A 5241 31 40 CBAx Cx Ax 3 12 4 C B A xxx xx 23 2 2 48 2)1(3 1 124 xxx
Пример dx xx 2 2)1(3 1 124 52 2 2)1(3 1 12452 x dx dxxdxdxx C x xxxx x 1 3 1 ln 12 ln
