γ+(90° +γ/2) =180°, vadinasi, γ = 60°. Šiuo atveju akordai O.A.
1
Ir OB 1
keturkampio apskritimas OA 1
NE 1
yra vienodi, nes turi vienodus kampus OCA
1
Ir DRUSKA 1
.
Įbrėžtas apskritimas Δ ABC liečia jo šonus vidiniuose taškuose. Išsiaiškinkime, kokie yra apskritimai, liečiantys tris linijas AB, BC Ir SA. Dviejų susikertančių linijų liestinės apskritimo centras yra vienoje iš dviejų tiesių, dalijančių kampus tarp pradinių linijų. Todėl apskritimų centrai, liečiantys tiesias linijas AB, BC Ir S A, guli ant trikampio išorinių arba vidinių kampų (arba jų plėtinių) pusiausvyros. Vidinio kampo pusiausvyra eina per bet kurių dviejų išorinių kampų bisektorių susikirtimo tašką. Šio teiginio įrodymas pažodžiui pakartoja atitinkamo teiginio vidaus kampų pusiausvyroms įrodymą. Dėl to gauname 4 apskritimus su centrais O, APIE A , Oi Ir APIE Su
(57 pav.). Apskritimas su centru APIE A
paliečia šoną Saulė Ir

vakarėlių tęsiniai AB Ir kintamoji srovė;šis ratas vadinamas neįrašytas
perimetras Δ ABC. Trikampio apskritimo spindulys paprastai žymimas r, o apskritimo spindulys r A ,
G b ir g Su .
Tarp įbrėžtųjų ir išorinių apskritimų spindulių galioja tokie ryšiai:
G /
g s =(р-с)/р ir G
G Su = (p - a) (p - b), Kur R- pusiau perimetras Δ ABC.Įrodykime tai. Tegul K ir L yra įbrėžtos ir apibrėžiamos tiesės liesties taškai Saulė(58 pav.). Dešinieji trikampiai SULČIOS Ir CO
c
L
todėl yra panašūs
G /
g s =Gerai/O Su L
=
CK
/
C.L.
..
Anksčiau buvo įrodyta, kad SC = (a+b-c)/2=p-c.
Belieka tai patikrinti C.L.
=
p
.
Leisti M Ir R- apskritimo su tiesiomis linijomis liesties taškai AB Ir AC. Tada
CL= (CL+CP)/ 2 = (CB+BL+CA+AP)/2 = (CB+BM + CA+AM)/2 = R
Norėdami įrodyti ryšį rr
c
=(p
-
a
)(p
-
b
)
apsvarstykite stačiuosius trikampius L.O.
C
B
Ir KVO, kurios yra panašios, nes
<OBK
+<
O
C
B.L.
=(<СВА + <АВ
L
)/2=90°.
Reiškia, L O s /ВL =BK /KO, t.y. rr
c
=
K.O.
·
L.O.
c
=
B.K.
·
B.L.
.
Belieka tai pastebėti VK=(a
+
c
-
b
)/2=
p
-
b
Ir B.L.
=
C.L.
-
C.B.
=
p
-
a
.
Atkreipkime dėmesį į dar vieną įdomų turtą (jau iš tikrųjų įrodyta kelyje). Tegul užrašas ir apibrėžimas liečia šoną AB taškuose N Ir M(58 pav.). Tada ESU.
=
BN
.
Iš tikrųjų, BN
=
p
-
b
Ir AM=AR=SR-AS=p – c.
Santykiai rr
c
=(p
- A) (p-V )
Ir r
p=r
Su (R-c) gali būti naudojamas Herono formulei gauti S
2
=
p
(p
-
a
)(p
-
b
)(p
-
c
),
Kur S
- trikampio plotas. Padauginę šiuos santykius, gauname r
2
p
=(p
-
a
)(p
-
b
)(p
-
c
).
Belieka tai patikrinti S
=
pr
.
Tai lengva padaryti nupjaunant Δ ABCįjungta ΔAOB,
ΔBOS Ir ΔSOA.

VIDURINĖS SANTYKOS TAŠKAS
Įrodykime, kad trikampio medianos susikerta viename taške. Norėdami tai padaryti, apsvarstykite esmę M, kur susikerta medianos AA 1
Ir BB 1
.
Atlikime Δ BB1S vidurio linija A
1
A
2
,
lygiagrečiai BB 1
(59 pav.). Tada A
1
M
:
ESU.
=
B
1
A
2
:
AB
1
=
B
1
A
2
:
B
1
C
=
B.A.
1
:VS=1:2, y., medianų susikirtimo taškas BB 1
Ir AA 1
dalija medianą AA 1
santykiu 1:2. Panašiai ir medianų susikirtimo taškas SS 1
Ir AA 1
dalija medianą AA 1
santykiu 1:2. Todėl medianų susikirtimo taškas AA 1
Ir BB 1
sutampa su medianų susikirtimo tašku AA 1
Ir SS 1
.
Jei trikampio medianų susikirtimo taškas yra sujungtas su viršūnėmis, tada trikampis bus padalintas į tris vienodo ploto trikampius. Išties, pakanka įrodyti, kad jeigu R- bet kuris medianos taškas AA 1
V ABC, tada sritis ΔAVR Ir ΔACP yra lygūs. Juk medianos AA 1
Ir RA 1
Δ ABC ir Δ RVS supjaustykite juos vienodo ploto trikampiais.
Teisingas ir atvirkštinis teiginys: jei tam tikru momentu R, guli viduje Δ ABC, plotas Δ AVR, Δ
TREČIADIENĮ Ir ΔSAR tada yra lygūs R- medianų susikirtimo taškas. Tiesą sakant, nuo sričių lygybės ΔAVR Ir ΔHRV iš to seka, kad atstumai nuo taškų A ir C iki tiesės VR yra lygūs, o tai reiškia VR eina per segmento vidurį AC. Dėl AR Ir SRįrodymas panašus.
Trikampių, į kuriuos medianos dalija trikampį, plotų lygybė leidžia rasti trikampio, sudaryto iš medianų, plotų s santykį taip: ΔABC,į paties Δ plotą S ABC. Leisti M- medianų susikirtimo taškas Δ ABC; taškas A" simetriškas A taško atžvilgiu M(60 pav.)
Viena vertus, sritis ΔA"MS lygus S/3. Kita vertus, šis trikampis sudarytas iš atkarpų, kurių kiekvieno ilgis yra lygus 2/3 atitinkamos medianos ilgio, taigi jo plotas
lygus (2/3) 2 s = 4s /9. Vadinasi, s
=3
S
/4.

Labai svarbi medianų susikirtimo taško savybė yra ta, kad trijų vektorių, einančių iš jo į trikampio viršūnes, suma yra lygi nuliui. Pirmiausia atkreipkime dėmesį į tai AM = 1/3(AB+AC), Kur M- medianų susikirtimo taškas Δ
ABC
.
Tiesą sakant, jei
ABA
"SU- tada lygiagretainis AA" = AB + AC Ir AM = 1/3AA".Štai kodėl MA+MV+MC=1/3(BA+SA+AB + SV + AC + BC) = 0.
Taip pat aišku, kad šią savybę turi tik medianų susikirtimo taškas, nes jeigu X
- Tada bet koks kitas taškas
HA+XB+XC=(XM+MA)+(XM+MV)+(XM+MS)=3ХМ..
Naudodami šią trikampio medianų susikirtimo taško savybę, galime įrodyti tokį teiginį: trikampio medianų susikirtimo taškas su viršūnėmis, esančiomis kraštinių vidurio taškuose. AB,CD
Ir E.F.
šešiakampis ABCDEF
sutampa su trikampio vidurių susikirtimo tašku su kraštinių vidurio taškais saulė,DE
Ir F.A.
.
Tiesą sakant, pasinaudojant tuo, kad jei pvz. R- segmento vidurys AB, tada bet kokiam taškui X
lygybė yra tiesa HA+ HB=2ХР, Nesunku įrodyti, kad abiejų nagrinėjamų trikampių medianų susikirtimo taškai turi savybę, kad vektorių, einančių iš jų į šešiakampio viršūnes, suma lygi nuliui. Todėl šie taškai sutampa.
Medianų susikirtimo taškas turi vieną savybę, kuri jį ryškiai išskiria iš kitų svarbių trikampio taškų: jei Δ A"B"C" yra projekcija ΔABCį plokštumą, tada medianų Δ susikirtimo taškas A "B" C"
yra medianų susikirtimo taško projekcija ΔABC tame pačiame lėktuve. Tai lengvai išplaukia iš to, kad projektuojant atkarpos vidurys patenka į jo projekcijos vidurį, o tai reiškia, kad trikampio mediana patenka į jo projekcijos medianą. Nei bisektorius, nei aukštis neturi šios savybės.
Pažymėtina, kad trikampio medianų susikirtimo taškas yra jo masės centras, tiek trijų materialių taškų, kurių masė yra vienodos masės, esančios trikampio viršūnėse, masės centras ir trikampio masės centras. tam tikro trikampio formos plokštelė. Savavališkame taške šarnyrinio trikampio pusiausvyros padėtis X
,
bus padėtis, kurioje spindulys HM nukreiptas į Žemės centrą. Trikampio, sujungto su medianų susikirtimo tašku, bet kuri padėtis yra pusiausvyros padėtis. Be to, trikampis, kurio vidurinis susikirtimo taškas remiasi į adatos galiuką, taip pat bus pusiausvyros padėtyje.
AUKŠČIŲ SANTYKOS TAŠKAS
Norėdami įrodyti, kad aukščiai Δ ABC susikerta viename taške, prisiminkite įrodinėjimo kelią, nubrėžtą skyriaus „Apriboto apskritimo centras“ pabaigoje. Perkelkime jus per viršūnes A, B Ir SU tiesios linijos, lygiagrečios priešingoms kraštinėms; šios linijos sudaro Δ A 1
IN 1
SU 1
(61 pav.). Aukštis Δ ABC yra statmenos šoninės pusės ΔA
1
B
1
C
1
.
Vadinasi, jie susikerta viename taške – apskritimo centre ΔA
1
B
1
C
1
.
Trikampio aukščių susikirtimo taškas kartais vadinamas jo ortocentras.
-
Nesunku patikrinti, ar H yra aukščių Δ susikirtimo taškas ABC, Tai A, B Ir SU - aukščio susikirtimo taškai Δ VNS, ΔSNA ir Δ ANV atitinkamai.
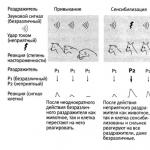
Taip pat aišku, kad<ABC
+ <
A.H.C.
=
180°, nes <
B.A.
1
H
= <
B.C.
1
H
=90° (A
1
Ir C
1
- aukščių pagrindai). Jei taškas H
1
simetriškas taškui H tiesės atžvilgiu kintamoji srovė, tada keturkampis ABCN 1
įrašytas. Vadinasi, apibrėžtųjų apskritimų spinduliai Δ ABC ir Δ AN S yra lygūs ir šie apskritimai yra simetriški šono atžvilgiu AC(62 pav.). Dabar tai lengva įrodyti
AN=a|ctg A|, kur a=BC. Iš tikrųjų,
AH=2R nuodėmė<
ACH=2R|cos A| =a|ctg A| .
Tarkime dėl paprastumo ΔABC smailaus kampo ir apsvarstykite Δ A
1
B
1
C
1
,
suformuotas jos aukštumų pagrindų. Pasirodo, kad įbrėžto apskritimo centras Δ A
1
B
1
C
1
yra aukščių Δ susikirtimo taškas ABC, ir išorinių apskritimų centrai


ΔA
1
B
1
C
1
yra Δ viršūnės ABC(63 pav.). Taškai A 1
Ir IN 1
CH(nuo kampų NV 1
S ir ON 1
SU tiesiai), taigi <
H.A.
1
B
1
= <
HCB
1
.
taip pat<H.A.
1
C
1
= <
HBC
1
.
Ir nuo tada<HCB
1
= =<
HBC
1
Tai A 1
A - bisektorius<IN 1
A 1
SU 1
.
Leisti N- aukščių susikirtimo taškas AA 1
, BB 1
Ir CC
1
trikampis ABC
.
Taškai A
1
Ir IN 1
guli ant apskritimo, kurio skersmuo AB,Štai kodėl A.H.
·
A
1
H
=
B.H.
·
B
1
H
. taip pat VNB
1
H
=CH ·C 1
N.
Smailiojo trikampio atveju teisingas ir atvirkštinis teiginys: jei taškai A 1, B
1
Ir C
1
gulėti ant šonų V. S., SA ir AB smailaus kampo Δ ABC ir segmentai AA 1
, BB 1
Ir SS 1
susikerta taške R, ir AR A 1
Р=ВР·В 1
P=CP·S 1
R, Tai R- aukščių susikirtimo taškas. Tiesą sakant, nuo lygybės
AP · A 1 P = BP · B 1 P
iš to seka, kad taškai A, B, A 1
Ir IN 1
guli ant to paties skersmens apskritimo AB, tai reiškia <
AB
1
B
= <
B.A.
1
A
=γ.
taip pat <
ACiC
=<
CAiA
=
β
Ir
<СВ
1
B=<ВС
1
C= α
(64 pav.). Taip pat aišku, kad α + β= CC
1
A
=
l
80°, β+γ=180° ir γ + α = 180°. Todėl α = β=γ=90°.
Trikampio aukščių susikirtimo tašką galima nustatyti kitu labai įdomiu būdu, tačiau tam mums reikia vektoriaus ir vektorių skaliarinės sandaugos sąvokų.
Leisti APIE- apibrėžtojo apskritimo centras Δ ABC. Vektorinė suma O A+ O.B.
+ OS yra tam tikras vektorius, taigi yra toks taškas R, Ką ARBA = OA + OB + OS. Paaiškėjo, kad R- aukščių susikirtimo taškas Δ ABC!
Pavyzdžiui, įrodykime tai AP
statmenai B.C.
.
Tai aišku AR=AO+
+op=ao+(oa+ov+os)=ov+os ir all= -ov+os.
Todėl vektorių skaliarinė sandauga AR Ir Saulė lygus OS 2
- O.B.
2
=
R
2
-
R
2
=0,
y., šie vektoriai yra statmeni.
Ši trikampio ortocentro savybė leidžia įrodyti kai kuriuos toli gražu neaiškius teiginius. Apsvarstykite, pavyzdžiui, keturkampį ABCD
,
įrašytas į apskritimą. Leisti Na, Nv, Ns Ir H
d
- ortocentrai Δ
BCD
, Δ
CDA
, Δ
DAB
ir Δ
ABC
atitinkamai. Tada atkarpų vidurio taškai AN A , VN, CH SU ,
D.H.
d
susilyginti. Tiesą sakant, jei APIE yra apskritimo centras ir M- segmento vidurys AN A ,
Tai OM=1/2(0A + OH A )= =1/2(OA + OB+OS+OD
)
.
Kitų trijų atkarpų vidurio taškams gauname lygiai tokias pačias išraiškas.
EULER DIRECT
Įspūdingiausia nuostabių taškų savybė yrakampas yra toks, kad kai kurie iš jų yra sujungti vienas su kitutam tikrais santykiais. Pavyzdžiui, susikirtimo taškas mediana M,
aukščių H ir apibrėžtojo apskritimo centro susikirtimo taškassavybės O yra toje pačioje tiesėje, o taškasM dalija segmentą JIS
kad santykis galiotųOM:MN= 1:2. Tai teoremą 1765 metais įrodė Leonhardas Euleris, kurisSavo nenuilstama veikla jis žymiai išplėtojo daugelį matematikos sričių ir padėjo pamatus daugeliui naujų jos šakų. Jis gimė 1707 metais Šveicarijoje. Būdamas 20 metų Euleris rekomendavoBroliai Bernoulli gavo kvietimą atvykti į Sankt Peterburgąburg, kur prieš pat buvo organizuota akademija. INpabaigoje Rusijoje dėl Anos Leopol atėjimo į valdžią 1740 mDovna, susiklostė nerimą kelianti situacija, ir Euleris persikėlė įBerlynas. Po 25 metų jis vėl grįžo į Rusiją, iš visoEuleris daugiau nei 30 metų gyveno Sankt Peterburge. Būdamas Burleyne, Euleris palaikė glaudžius ryšius su Rusijos akademija ir buvojos garbės narys. Iš Berlyno Euleris susirašinėjo su Lomonopelėdos Jų susirašinėjimas prasidėjo taip. 1747 metais Lomonosovas buvo išrinktas profesoriumi, tai yra tikruoju akademijos nariu; Imperatorė patvirtino šiuos rinkimus. Po toreakcingas akademijos pareigūnas Schumacheris, kuris įnirtingai nekenčia teisėsMonosovas išsiuntė savo darbą Euleriui, tikėdamasis gauti informacijos apie juosbloga apžvalga. (Euleris buvo tik 4 metais vyresnis už Lomonosovą,bet tuo metu jo mokslinis autoritetas jau buvo labai aukštas.)Savo apžvalgoje Euleris rašė: „Visi šie darbai yra ne tik gerishi, bet ir puikiai, nes jis paaiškina fizinius ir cheminius būtiniausius ir sunkiausius reikalus, kurie visiškai nežinomi ir interpretacijos buvo neįmanomosšmaikščiausiems ir išmokusiemsžinomų žmonių, su tokiu įkūrėjudalykas, dėl kurio esu visiškai tikrasjo parodymų tikslumas...Reikia visko norėtikurios akademijos sugebėjo parodyti tokius išradimus, kadkurį parodė ponas Lomo nosis“.
Pereikime prie įrodymo Eilerio teorema. Pasvarstykime Δ
A
1
B
1
C
1
su viršūnėmis  kraštinių vidurio taškai Δ ABC; leisti H
1
ir H yra jų ortocentrai (65 pav.). Taškas H 1 sutampa su centru APIE apskritimas Δ ABC.Įrodykime, kad Δ C
1
H
1
M
=Δ
CHM
.
Iš tiesų, pagal medianų susikirtimo taško savybę SU 1
M:
CM= 1:2, panašumo koeficientas Δ A
1
B
1
C
1
ir Δ ABC yra lygus 2, taigi C
1
H
1
:
CH
=1:2,
Be to,<H
1
C
1
M
=<НСМ (C
1
H
1
||
CH
).
Todėl,< C
1
M.H.
1
= < SMN, o tai reiškia tašką M guli ant segmento H
1
H
.
Be to, H
1
M
:
M.H.
=1:2,
kadangi panašumo koeficientas Δ C
1
H
1
M
ir Δ SNM lygus 2.
kraštinių vidurio taškai Δ ABC; leisti H
1
ir H yra jų ortocentrai (65 pav.). Taškas H 1 sutampa su centru APIE apskritimas Δ ABC.Įrodykime, kad Δ C
1
H
1
M
=Δ
CHM
.
Iš tiesų, pagal medianų susikirtimo taško savybę SU 1
M:
CM= 1:2, panašumo koeficientas Δ A
1
B
1
C
1
ir Δ ABC yra lygus 2, taigi C
1
H
1
:
CH
=1:2,
Be to,<H
1
C
1
M
=<НСМ (C
1
H
1
||
CH
).
Todėl,< C
1
M.H.
1
= < SMN, o tai reiškia tašką M guli ant segmento H
1
H
.
Be to, H
1
M
:
M.H.
=1:2,
kadangi panašumo koeficientas Δ C
1
H
1
M
ir Δ SNM lygus 2.
DEVYNIŲ TAŠKŲ ratas
1765 m. Euleris atrado, kad trikampio kraštinių vidurio taškai ir jo aukščio pagrindai yra tame pačiame apskritime. Įrodysime ir šią trikampio savybę.
Tegul B 2 yra aukščio, nukritusio iš viršaus, pagrindas INįjungta
pusėje AC. Taškai IN ir B 2 yra simetriški tiesei linijai A 1
SU 1
(66 pav.). Todėl Δ A
1
IN
2
SU
1
= Δ
A
1
B.C.
t
= Δ
A
1
B
1
C
1
,
Štai kodėl <
A
1
B
2
C
1
= <А
1
IN 1
SU 1
,
o tai reiškia tašką IN 2
guli ant aprašyto
ratas ΔA
1
IN
1
SU
1
.
Likusiems aukščių pagrindams įrodymas yra panašus. „

Vėliau buvo nustatyta, kad tame pačiame apskritime yra dar trys taškai - atkarpų, jungiančių ortocentrą su trikampio viršūnėmis, vidurio taškai. Štai kas yra devynių taškų apskritimas.
Leisti Az Ir NW- atkarpų vidurio taškai AN Ir CH, S 2
- nuo viršaus nukrito aukščio pagrindas SUįjungta AB(67 pav.). Pirmiausia tai įrodykime A
1
C
1
A
3
C
3
- stačiakampis. Tai lengvai išplaukia iš to, kad A 1
NW Ir A
3
C
1
- vidurio linijos Δ VSN Ir ΔAVN, A A
1
C
1
Ir A 3
NW- vidurio linijos Δ ABC ir Δ ASN. Todėl taškai A 1
Ir Az guli ant apskritimo, kurio skersmuo SU 1
ŠV, ir nuo tada Az Ir NW guli ant apskritimo, einančio per taškus A 1,
C
1
ir C 2. Šis apskritimas sutampa su Eulerio nagrinėjamu apskritimu (jei Δ ABC ne lygiašonis). Dėl taško Vzįrodymas panašus.
TORRICELLI TAŠKAS
Savavališko keturkampio viduje ABCD
Nesunku rasti tašką, kurio atstumų suma iki viršūnių turi mažiausią reikšmę. Toks taškas yra taškas APIE jo įstrižainių sankirta. Tiesą sakant, jei X
- Tada bet koks kitas taškas AH+HS≥AC=AO+OS Ir BX
+
XD
≥
BD
=
B.O.
+
O.D.
,
ir bent viena iš nelygybių yra griežta. Trikampio atveju panašią problemą išspręsti sunkiau; Paprastumo dėlei apsvarstysime ūmaus trikampio atvejį.
Leisti M- tam tikras taškas smailaus kampo Δ viduje ABC. Apverskime Δ ABC kartu su tašku M 60° aplink tašką A(68 pav.). (Tiksliau, tegul B, C Ir M"- taškų vaizdai B, C Ir M pasukus 60° aplink tašką A.) Tada AM+VM+SM=MM"+B.M.
+
C
"
M
", AM = MM", Taigi kaip ΔAMM- lygiašoniai (AM = AM") Ir<MAM" = 60°. Dešinė lygybės pusė yra trūkinės linijos ilgis VMM"S"
;
jis bus mažiausias, kai ši nutrūkusi linija

sutampa su segmentu Saulė"
.
Tokiu atveju<.
A.M.B.
=
180° -<AMM" = 120° ir<АМС = <ESU.
"
C
-
180°-<ESU.
"
M
=
120°, t.y. šonai AB, BC ir SA matomi iš taško M 120° kampu. Toks taškas M paskambino Torricelli taškas trikampis ABC
.
Tačiau įrodykime, kad smailiojo trikampio viduje visada yra taškas M, iš kurių kiekviena pusė matoma 120° kampu. Pastatykime jį šone AB trikampis ABC
išoriškai teisingas Δ ABC 1
(69 pav.). Leisti M-apskritimo apskritimo susikirtimo taškas ΔABC 1
ir tiesiai SS 1
.
Tada ABC
1
=60° Ir ABC matomas iš taško M 120° kampu. Tęsdami šiuos argumentus šiek tiek toliau, galime gauti kitą Torricelli taško apibrėžimą. Sukurkime taisyklingus trikampius A 1
Saulė Ir AB 1
SU taip pat ginkluotųjų pajėgų pusėse ir AC.Įrodykime, kad taškas M taip pat yra tiesėje AA 1
.
Tikrai taškas M guli ant apskritimo Δ A
1
B.C.
,
Štai kodėl<A
1
M.B.
= <
A
1
C.B.
= 60°, tai reiškia<A 1
MV+<.
B.M.A.
=
180°. Taip pat taškas M guli ant tiesios linijos BB 1
(69 pav.).
Viduje Δ ABC yra vienas taškas M, iš kurio jo kraštinės matomos 120° kampu, nes apibrėžti apskritimai Δ ABC
1
, Δ
AB
i
C
ir Δ A
1
Saulė negali turėti daugiau nei vieno bendro taško.
Dabar pateiksime fizinę (mechaninę) Torricelli taško interpretaciją. Užfiksuokime Δ viršūnėse ABCžiedus, per juos praleidžiame tris virves, kurių vienas galas surišamas, o ant kitų galų tvirtinami vienodos masės kroviniai (70 pav.). Jeigu x = MA, y = MV,z
=
M.C.
Ir A yra kiekvieno sriegio ilgis, tada nagrinėjamos sistemos potencinė energija lygi m g
(x
-A)+ m g
(y
-
a
)+
mg
(z
--A). Pusiausvyros padėtyje potenciali energija turi mažiausią reikšmę, todėl suma x+y+z taip pat turi mažiausią reikšmę. Kita vertus, pusiausvyros padėtyje jėgų rezultatas taške M lygus nuliui. Šios jėgos yra lygios absoliučiu dydžiu, todėl poriniai kampai tarp jėgos vektorių yra lygūs 120°.

Belieka pasakyti, kaip viskas yra buku trikampio atveju. Jei bukas kampas yra mažesnis nei 120°, tada visi ankstesni argumentai lieka galioti. O jei bukas kampas yra didesnis arba lygus 120°, tai atstumų nuo trikampio taško iki jo viršūnių suma bus mažiausia, kai šis taškas yra bukojo kampo viršūnė.
BROKARDO TAŠKAI
Brocard taškai Δ ABC tokie vidiniai taškai vadinami R Ir K
,
Ką<GKŠP
= <.
BCP
=<
BŽŪP
Ir<.
QAB
= <.
QBC
= < QCA
(lygiakraščio trikampio Brokardo taškai susilieja į vieną tašką). Įrodykime, kad bet kurio Δ viduje ABC yra taškas R, turintis reikiamą savybę (taškui K
įrodymas panašus). Pirmiausia suformuluokime Brocard taško apibrėžimą kita forma. Pažymime kampo reikšmes, kaip parodyta 71 paveiksle<ARV=180° - a+x-y, lygybė x=y yra lygiavertis lygybei<APB
=180°-<
.
A
.
Vadinasi, R- taškas Δ ABC, iš kurių pusių AB,
Saulė Ir SA matomas 180° kampu -<.
A
,
180°-<B
,
180°-<SU.
Tokį tašką galima sukonstruoti taip. Kurkime toliau
pusėje Saulė trikampis ABC panašus trikampis CA1B
kaip parodyta 72 paveiksle. Įrodykime, kad tiesės susikirtimo taškas P AA1 ir apibraukti ΔA1BC ieškomas. Faktiškai,<BPC
=18
O
° - β
Ir<APB
=
180°-<A
t
P.B.
=
180° -<A
1
C.B.
=
l
80°- A. Toliau panašiu būdu sukurkime panašius trikampius iš šonų AC Ir AB(73 pav.). Nes<.
APB
=
180° - A, taškas R taip pat guli ant apskritimo Δ ABC 1
Vadinasi,<BPC
1
= <BAC
1
= β, o tai reiškia tašką
R guli ant segmento SS 1
.
Jis taip pat yra ant segmento BB 1
,
t.y. R - atkarpų susikirtimo taškas AA 1
, BB 1
Ir SS 1
.
Brocardo mintis R turi tokią įdomią savybę. Leiskite tiesiai AR, VR Ir SR susikerta su apskritimu ΔABC


taškuose A 1, B 1 ir C 1 (74 pav.). Tada Δ ABC = Δ
B
1
SU 1
A
1
.IN faktiškai,<.
A
1
B
1
C
1
= <
A
1
B
1
B
+ <
BB 1 C 1 =<A
1
AB
+<В
CC 1 =<A
1
AB
+ +<
A
1
A.C.
=<.ВАС,
pagal Brokardo taško ΔABC savybę kampai BCC 1 ir A 1 AC yra lygūs, o tai reiškia A
1
C
1
=
B.C.
.
Likusių kraštinių lygybė Δ ABC ir Δ B 1 C 1 A 1 tikrinami tokiu pat būdu.
Visais mūsų nagrinėtais atvejais įrodymas, kad atitinkami tiesių trigubai susikerta viename taške, gali būti atliktas naudojant Cevos teorema. Suformuluosime šią teoremą.
Teorema. Leiskite į šonus AB, BC Ir S A trikampis ABC
paimtų taškų SU 1
, A 1
Ir IN 1
atitinkamai. Tiesioginis AA 1
, BB 1
Ir SS 1
susikerta viename taške tada ir tik tada
AC 1 / C 1 V VA 1 / A 1 C SV 1 / V 1 A = 1.
Teoremos įrodymas pateiktas L.S. Atanasyano geometrijos vadovėlyje 300 p.
Literatūra.
1.Atanasyan L.S. Geometrija 7-9.- M.: Išsilavinimas, 2000 m.
2. Kiselevas A.P. Elementarioji geometrija – M.: Išsilavinimas, 1980 m.
3. Nikolskaya I.L. Pasirenkamas matematikos kursas. M.: Išsilavinimas, 1991 m.
4. Jaunojo matematiko enciklopedinis žodynas... Comp. A.P.Savin.-.M.: Pedagogika, 1989 m.
Sverdlovsko srities bendrojo ir profesinio švietimo ministerija.
Jekaterinburgo savivaldybės švietimo įstaiga.
Mokymo įstaiga – MOUSOSH Nr. 212 „Jekaterinburgo kultūros licėjus“
Ugdymo sritis – matematika.
Tema – geometrija.
Įspūdingi trikampio taškai
Referentas: 8 klasės mokinys
Selitskis Dmitrijus Konstantinovičius.
Mokslinis patarėjas:
Rabkanovas Sergejus Petrovičius.
Jekaterinburgas, 2001 m
Įvadas 3
Aprašomoji dalis:
Ortocentras 4
Ledo centras 5
Svorio centras 7
Circumcenter 8
Eulerio 9 eilutė
Praktinė dalis:
Ortocentrinis trikampis 10
11 išvada
Literatūra 11
Įvadas.
Geometrija prasideda nuo trikampio. Du su puse tūkstantmečio trikampis buvo geometrijos simbolis. Jo naujos savybės nuolat atrandamos. Norint kalbėti apie visas žinomas trikampio savybes, prireiks daug laiko. Mane domino vadinamieji „Įspūdingi trikampio taškai“. Tokių taškų pavyzdys yra bisektorių susikirtimo taškas. Įspūdinga yra tai, kad jei paimsite tris savavališkus erdvės taškus, iš jų sukursite trikampį ir nubrėžsite pusiausvyras, tada jie (pusiauliai) susikirs viename taške! Atrodytų, tai neįmanoma, nes paėmėme savavališkus taškus, tačiau ši taisyklė galioja visada. Kiti „įdomūs taškai“ turi panašių savybių.
Perskaitęs literatūrą šia tema, aš pataisiau sau penkių nuostabių taškų ir trikampio apibrėžimus ir savybes. Tačiau mano darbas tuo nesibaigė, norėjau pats ištirti šiuos dalykus.
Štai kodėl taikinysŠis darbas yra kai kurių puikių trikampio savybių tyrimas ir ortocentrinio trikampio tyrimas. Siekiant šio tikslo, galima išskirti šiuos etapus:
Literatūros parinkimas, padedant mokytojui
Pagrindinių trikampio taškų ir linijų savybių tyrimas
Šių savybių apibendrinimas
Ortocentrinio trikampio uždavinio sudarymas ir sprendimas
Pristačiau šiame tiriamajame darbe gautus rezultatus. Visus brėžinius dariau naudodamas kompiuterinę grafiką (vektorinės grafikos redaktorius CorelDRAW).
Ortocentras. (Aukščių susikirtimo taškas)
Įrodykime, kad aukščiai susikerta viename taške. Perkelkime jus per viršūnes A, IN Ir SU trikampis ABC tiesios linijos, lygiagrečios priešingoms kraštinėms. Šios linijos sudaro trikampį A 1
IN 1
SU 1
. trikampio aukštis ABC yra statmenos trikampio kraštinėms A 1
IN 1
SU 1
. todėl jie susikerta viename taške – trikampio apskritimo centre A 1
IN 1
SU 1
. Trikampio aukščių susikirtimo taškas vadinamas ortocentru ( H).
Icentras yra įbrėžto apskritimo centras.
(Šiaulių sankirtos taškas)

Įrodykime, kad trikampio kampų pusiausvyros ABC susikerta viename taške. Apsvarstykite esmę APIE kampo bisektoriaus sankirtos A Ir IN. bet kurie kampo A pusiausvyros taškai yra vienodu atstumu nuo tiesių AB Ir AC, ir bet kuris kampo bisektoriaus taškas IN vienodu atstumu nuo tiesių AB Ir Saulė, taigi taškas APIE vienodu atstumu nuo tiesių AC Ir Saulė, t.y. jis guli ant kampo pusiausvyros SU. taškas APIE vienodu atstumu nuo tiesių AB,
Saulė Ir SA, o tai reiškia, kad yra apskritimas su centru APIE, šių linijų liestinė, o lietimo taškai yra pačiose šonuose, o ne jų tęsiniuose. Tiesą sakant, kampai viršūnėse A Ir IN trikampis AOB aštrus todėl projekcijos taškas APIE tiesiogiai AB yra segmento viduje AB.
Vakarėliams Saulė Ir SAįrodymas panašus.
Centras turi tris savybes:

Jei kampo bisektoriaus tęsinys SU kerta trikampio apskritimą ABC taške M, Tai MA=MV=MO.

Jeigu AB- lygiašonio trikampio pagrindas ABC, tada apskritimo liestinė kampo kraštinėms DIA taškuose A Ir IN, eina per tašką APIE.

Jei tiesė, einanti per tašką APIE lygiagrečiai šonui AB, kerta šonus Saulė Ir SA taškuose A 1
Ir IN 1
, Tai A 1
IN 1
=A 1
IN+AB 1
.
Gravitacijos centras. (medianų susikirtimo taškas)

Įrodykime, kad trikampio medianos susikerta viename taške. Norėdami tai padaryti, apsvarstykite esmę M, kurioje susikerta medianos AA 1
Ir BB 1
. nubrėžkime trikampį BB 1
SU vidurio linija A 1
A 2
, lygiagrečiai BB 1
. Tada A 1
M:AM=IN 1
A 2
: AB 1
=IN 1
A 2
:IN 1
SU=VA 1
: SAULE=1:2, t.y. medianinis susikirtimo taškas BB 1
Ir AA 1
dalija medianą AA 1
santykiu 1:2. Panašiai ir medianų susikirtimo taškas SS 1
Ir AA 1
dalija medianą AA 1
santykiu 1:2. Todėl medianų susikirtimo taškas AA 1
Ir BB 1
sutampa su medianų susikirtimo tašku AA 1
Ir SS 1
.
Jei trikampio medianų susikirtimo taškas yra sujungtas su viršūnėmis, tada trikampiai bus padalinti į tris vienodo ploto trikampius. Išties, pakanka įrodyti, kad jeigu R– bet kuris medianos taškas AA 1
trikampyje ABC, tada trikampių plotai AVR Ir AKR yra lygūs. Juk medianos AA 1
Ir RA 1
trikampiuose ABC Ir RVS supjaustykite juos vienodo ploto trikampiais.
Teisingas ir atvirkštinis teiginys: jei tam tikru momentu R, guli trikampio viduje ABC, trikampių plotas AVR, TREČIADIENĮ Ir SAR tada yra lygūs R– medianų susikirtimo taškas.
Susikirtimo taškas turi dar vieną savybę: jei iš bet kokios medžiagos iškirpsite trikampį, ant jo nubraižysite medianas, medianų susikirtimo taške pritvirtinsite strypą ir pritvirtinsite pakabą ant trikojo, tada modelis (trikampis) atsidurs pusiausvyros būsena, todėl susikirtimo taškas yra ne kas kita, kaip trikampio svorio centras.
Apriboto apskritimo centras.

Įrodykime, kad yra taškas, nutolęs vienodu atstumu nuo trikampio viršūnių, arba, kitaip tariant, kad yra apskritimas, einantis per tris trikampio viršūnes. Taškų, esančių vienodu atstumu nuo taškų, vieta A Ir IN, yra statmena atkarpai AB, einantis per jo vidurį (statmena atkarpai AB). Apsvarstykite esmę APIE, kurioje kertasi statmenų į atkarpas pusiaukampės AB Ir Saulė. Taškas APIE vienodu atstumu nuo taškų A Ir IN, taip pat iš taškų IN Ir SU. todėl jis yra vienodu atstumu nuo taškų A Ir SU, t.y. jis taip pat guli ant atkarpai statmenos pusės AC.
centras APIE Apskritimas yra trikampio viduje tik tuo atveju, jei trikampis yra smailus. Jei trikampis yra stačiakampis, tada taškas APIE sutampa su hipotenuzės viduriu, o jei kampas viršūnėje SU bukas tada tiesus AB atskiria taškus APIE Ir SU.

Matematikoje dažnai nutinka taip, kad visiškai skirtingais būdais apibrėžti objektai pasirodo esą vienodi. Parodykime tai pavyzdžiu.
Leisti A 1
,
IN 1
,SU 1
– kraštinių vidurio taškai Saulė,SA ir AB. Galima įrodyti, kad apriboti trikampių apskritimai AB 1
SU,
A 1
Saulė 1
Ir A 1
IN 1
SU 1
susikerta viename taške, o šis taškas yra trikampio apskritimo centras ABC. Taigi, mes turime du iš pažiūros visiškai skirtingus taškus: statmenų bisektorių ir trikampio kraštinių susikirtimo tašką ABC o trikampių apskritimų susikirtimo taškas AB 1
SU 1
,
A 1
Saulė Ir A 1
IN 1
SU 1
. bet pasirodo, kad šie du taškai sutampa.
Eilerio tiesė.

Įspūdingiausia nuostabių trikampio taškų savybė yra ta, kad kai kurie iš jų yra sujungti vienas su kitu tam tikrais ryšiais. Pavyzdžiui, svorio centras M, ortocentras N ir apskritimo centras APIE guli toje pačioje tiesėje, o taškas M padalija atkarpą OH taip, kad ryšys galiotų OM: MN=1:2. Šią teoremą 1765 metais įrodė šveicarų mokslininkas Leonardo Euleris.
Ortocentrinis trikampis.

Ortocentrinis trikampis(stačiakampis) yra trikampis ( MNKAM), kurios viršūnės yra šio trikampio aukščių bazės ( ABC). Šis trikampis turi daug įdomių savybių. Padovanokime vieną iš jų.
Nuosavybė.
Įrodykite:
Trikampiai AKM, CMN Ir BKN panašus į trikampį ABC;
Stačiakampio kampai MNK yra: L
KNM
= π - 2
L
A,LKMN
=
π – 2 L
B,
L
MNK
= π - - 2 L
C.
Įrodymas:
Mes turime AB cos A, A.K. cos A. Vadinasi, ESU./AB
= A.K./A.C..
Nes ties trikampiais ABC Ir AKM kampas A– bendri, tada jie panašūs, iš to darome išvadą, kad kampas L
AKM
= L
C. Štai kodėl L
BKM
= L
C. Toliau turime L
MKC= π/2 – L
C, L
NKC= π/2 – – – L
C, t.y. SK– kampo bisektorius MNK. Taigi, L
MNK= π – 2 L
C. Likusios lygybės įrodomos panašiai.
Išvada.
Šio tyrimo pabaigoje galima padaryti tokias išvadas:
Svarbiausi trikampio taškai ir linijos yra:
ortocentras trikampio yra jo aukščių susikirtimo taškas;
ir centras trikampis yra pusiausvyros susikirtimo taškas;
gravitacijos centras trikampio yra jo medianų susikirtimo taškas;
cirkumcentras– yra pusiausvyros statmenų susikirtimo taškas;
Eilerio tiesi linija- tai tiesi linija, ant kurios yra svorio centras, ortocentras ir apskritimo centras.
Ortocentrinis trikampis padalija nurodytą trikampį į tris panašius trikampius.
Atlikęs šį darbą daug sužinojau apie trikampio savybes. Šis darbas man buvo aktualus matematikos srities žinių tobulinimo požiūriu. Ateityje ketinu plėtoti šią įdomią temą.
Bibliografija.
Kiseliovas A.P. Elementarioji geometrija. – M.: Išsilavinimas, 1980 m.
Coxeter G.S., Greitzer S.L. Nauji susitikimai su geometrija. – M.: Nauka, 1978 m.
Prasolovas V.V. Planimetrijos problemos. – M.: Nauka, 1986. – 1 dalis.
Sharygin I.F. Geometrijos problemos: planimetrija. – M.: Nauka, 1986 m.
Scanavi M.I. Matematika. Problemos su sprendimais. – Rostovas prie Dono: Feniksas, 1998 m.
Bergeris M. Geometrija dviejuose tomuose – M: Mir, 1984 m.
Turinys
Įvadas…………………………………………………………………………………3
1 skyrius.
1.1 Trikampis…………………………………………………………………………………..4
1.2.
Trikampio medianos
1.4. Aukštis trikampyje
Išvada
Naudotos literatūros sąrašas
Knygelė
Įvadas
Geometrija yra matematikos šaka, nagrinėjanti įvairias figūras ir jų savybes. Geometrija prasideda nuo trikampio. Du su puse tūkstantmečio trikampis buvo geometrijos simbolis; bet tai ne tik simbolis, trikampis yra geometrijos atomas.
Savo darbe nagrinėsiu trikampio pusiausvyros, medianų ir aukščių susikirtimo taškų savybes, pakalbėsiu apie jų išskirtines savybes ir trikampio linijas.
Tokie taškai, kurie buvo tiriami mokyklos geometrijos kurse, yra šie:
a) bisektorių susikirtimo taškas (įbrėžto apskritimo centras);
b) bisektoriaus statmenų susikirtimo taškas (apibrėžtojo apskritimo centras);
c) aukščių susikirtimo taškas (ortocentras);
d) medianų susikirtimo taškas (centroidas).
Aktualumas:
išplėsti savo žinias apie trikampį,jo savybesnuostabių taškų.
Tikslas:
trikampio tyrinėjimas iki jo puikių taškų,juos studijuojantklasifikacijos ir savybės.
Užduotys:
1. Studijuoti reikiamą literatūrą
2. Išstudijuokite žymiųjų trikampio taškų klasifikaciją
3. Gebėti sukonstruoti puikius trikampio taškus.
4. Apibendrinkite studijuotą medžiagą knygelės dizainui.
Projekto hipotezė:
galimybė rasti puikių taškų bet kuriame trikampyje leidžia išspręsti geometrines konstrukcijos problemas.
1 skyrius.
Istorinė informacija apie nuostabius trikampio taškus
Ketvirtojoje elementų knygoje Euklidas išsprendžia uždavinį: „Įrašyti apskritimą duotame trikampyje“. Iš sprendinio matyti, kad trys trikampio vidinių kampų pusiausvyros susikerta viename taške – įbrėžto apskritimo centre. Iš kitos Euklido uždavinio sprendimo matyti, kad į trikampio kraštines atstatyti statmenys jų vidurio taškuose taip pat susikerta viename taške – apibrėžtojo apskritimo centre. Elementai nesako, kad trys trikampio aukščiai susikerta viename taške, vadinamame ortocentru (graikiškas žodis „orthos“ reiškia „tiesus“, „teisinga“). Tačiau šį pasiūlymą žinojo Archimedas, Pappas ir Proklas.
Ketvirtasis trikampio vienaskaitos taškas yra medianų susikirtimo taškas. Archimedas įrodė, kad tai yra trikampio svorio centras (baricentras). Minėti keturi taškai sulaukė ypatingo dėmesio, o nuo XVIII amžiaus jie buvo vadinami „ypatingais“ arba „ypatingais“ trikampio taškais.
Su šiais ir kitais taškais susieto trikampio savybių tyrimas buvo pradžia kuriant naują elementariosios matematikos šaką - „trikampio geometriją“ arba „naują trikampio geometriją“, kurių vienas iš įkūrėjų buvo Leonhardas Euleris. 1765 m. Euleris įrodė, kad bet kuriame trikampyje ortocentras, baricentras ir cirkumcentras yra toje pačioje tiesėje, vėliau vadinamoje „Eulerio tiesia linija“.
Trikampis
Trikampis
- geometrinė figūra, susidedanti iš trijų taškų, kurie nėra toje pačioje tiesėje, ir trys atkarpos, jungiančios šiuos taškus poromis. Taškai -viršūnės
trikampis, segmentai -pusės
trikampis.
IN
A, B, C – viršūnės
AB, BC, SA - šonai
A C
Kiekvienas trikampis turi keturis su juo susijusius taškus:
Medianų susikirtimo taškas;
Bisektorių susikirtimo taškas;
Aukščių susikirtimo taškas.
Statmenų bisektorių susikirtimo taškas;
1.2.
Trikampio medianos
trikampio medina - , jungiantis viršūnę nuo priešingos pusės vidurio (1 pav.). Taškas, kuriame mediana kerta trikampio kraštinę, vadinamas medianos pagrindu.

1 pav. Trikampio medianos
Sukonstruokime trikampio kraštinių vidurio taškus ir nubrėžkime atkarpas, jungiančias kiekvieną viršūnę su priešingos kraštinės vidurio tašku. Tokie segmentai vadinami medianomis.
Ir vėl pastebime, kad šios atkarpos susikerta viename taške. Jei išmatuosime gautų medianų atkarpų ilgius, galime patikrinti dar vieną savybę: medianų susikirtimo taškas, skaičiuojant nuo viršūnių, padalija visas medianas santykiu 2:1. Ir vis dėlto trikampis, kuris remiasi ant adatos galo medianų susikirtimo taške, yra pusiausvyroje! Taškas, turintis šią savybę, vadinamas svorio centru (baricentru). Vienodos masės centras kartais vadinamas centroidu. Todėl trikampio medianų savybes galima suformuluoti taip: trikampio medianos susikerta svorio centre ir yra padalintos iš susikirtimo taško santykiu 2:1, skaičiuojant nuo viršūnės.
1.3. Trikampio pusiausvyros
Bisektorius paskambino kampo, nubrėžto nuo kampo viršūnės iki jo susikirtimo su priešinga kraštine, bisektorius. Trikampis turi tris bisektorius, atitinkančius tris jo viršūnes (2 pav.).

2 pav. Trikampio bisektorius
Savavališkame trikampyje ABC nubrėžiame jo kampų pusiausvyras. Ir vėl, esant tiksliai konstrukcijai, visi trys bisektoriai susikirs viename taške D. Taškas D taip pat neįprastas: jis yra vienodu atstumu nuo visų trijų trikampio kraštinių. Tai galima patikrinti nuleidus statmenus DA 1, DB 1 ir DC1 į trikampio kraštines. Visi jie yra lygūs vienas kitam: DA1=DB1=DC1.
Jei nubrėžiate apskritimą, kurio centras yra taške D, o spindulys DA 1, tada jis palies visas tris trikampio kraštines (tai yra, su kiekviena iš jų bus tik vienas bendras taškas). Toks apskritimas vadinamas įbrėžtu trikampyje. Taigi, trikampio kampų pusiausvyros susikerta įbrėžto apskritimo centre.
1.4. Aukštis trikampyje
trikampio aukštis - , nukrito iš viršaus į priešingą pusę arba tiesią liniją, sutampančią su priešinga puse. Priklausomai nuo trikampio tipo, aukštis gali būti įtrauktas į trikampį (už trikampis), sutampa su jo kraštine (be trikampis) arba išeina už trikampio ribų ties buku trikampiu (3 pav.).



3 pav. Trikampių aukščiai
Jei trikampyje pastatysite tris aukščius, tada jie visi susikirs viename taške H. Šis taškas vadinamas ortocentru. (4 pav.).
Naudodami konstrukcijas galite patikrinti, ar priklausomai nuo trikampio tipo, ortocentras yra skirtingai:
ūminiam trikampiui - viduje;
stačiakampiui - ant hipotenuzės;
buku kampu jis yra išorėje.

4 pav. Trikampio stačiakampis
Taigi, mes susipažinome su dar vienu nuostabiu trikampio tašku ir galime pasakyti, kad: trikampio aukščiai susikerta ties stačiakampiu.
1.5. Statmenos trikampio kraštinėms
Atkarpos statmuo yra tiesė, statmena nurodytai atkarpai ir einanti per jos vidurio tašką.
Nubraižykime savavališką trikampį ABC ir į jo kraštines nubrėžkime statmenas dvikampes. Jei konstrukcija bus atlikta tiksliai, tada visi statmenys susikirs viename taške - taške O. Šis taškas yra vienodu atstumu nuo visų trikampio viršūnių. Kitaip tariant, jei nubrėžiate apskritimą, kurio centras yra taške O, einantį per vieną iš trikampio viršūnių, tada jis taip pat eis per kitas dvi viršūnes.
Apskritimas, einantis per visas trikampio viršūnes, vadinamas apie jį apibrėžtuoju. Todėl nustatytą trikampio savybę galima suformuluoti taip: į trikampio kraštines statmenos pusės susikerta apibrėžtojo apskritimo centre (5 pav.).
 5 pav. Į apskritimą įbrėžtas trikampis
5 pav. Į apskritimą įbrėžtas trikampis
2 skyrius. Įspūdingųjų trikampio taškų tyrimas.
Aukščio tyrimas trikampiuose
Visos trys trikampio aukščiai susikerta viename taške. Šis taškas vadinamas trikampio ortocentru.

Ūmaus trikampio aukščiai yra griežtai trikampio viduje.
Atitinkamai, aukščių susikirtimo taškas taip pat yra trikampio viduje.
Stačiakampiame trikampyje du aukščiai sutampa su kraštinėmis. (Tai aukščiai, nubrėžti nuo smailių kampų viršūnių iki kojų).
Hipotenuzės aukštis yra trikampio viduje.
AC yra aukštis, nubrėžtas nuo viršūnės C iki kraštinės AB.
AB yra aukštis, nubrėžtas nuo viršūnės B iki AC pusės.
AK yra aukštis, nubrėžtas nuo stačiojo kampo viršūnės A iki hipotenuzės BC.
Stačiojo trikampio altitudės susikerta ties stačiojo kampo viršūne (A yra ortocentras).
Bukajame trikampyje trikampio viduje yra tik vienas aukštis – ta, kuri nubrėžta iš bukojo kampo viršūnės.
Kiti du aukščiai yra už trikampio ribų ir yra nuleisti iki trikampio kraštinių tęsinio.
AK yra aukštis, nubrėžtas į kraštą BC.
BF – aukštis, nubrėžtas į šoninės AC tęsinį.
CD yra aukštis, nubrėžtas į kraštinės AB tęsinį.
Bukojo trikampio aukščių susikirtimo taškas taip pat yra už trikampio ribų:
H yra trikampio ABC stačiakampis.
Trikampio pusiausvyros tyrimas
Trikampio pusiausvyra yra trikampio kampo (spindulio) pusiausvyros dalis, esanti trikampio viduje.
 Visos trys trikampio pusiausvyros susikerta viename taške.
Visos trys trikampio pusiausvyros susikerta viename taške.


Smailiame, bukajame ir stačiakampyje trikampių pusiaukelių susikirtimo taškas yra įbrėžto trikampio apskritimo centras ir yra viduje.
Medianų tyrimas trikampyje
Kadangi trikampis turi tris viršūnes ir tris kraštines, taip pat yra trys atkarpos, jungiančios viršūnę ir priešingos kraštinės vidurį.



Išnagrinėjęs šiuos trikampius, supratau, kad bet kuriame trikampyje medianos susikerta viename taške. Šis taškas vadinamas trikampio svorio centras.
Statmenų trikampio kraštinei tyrimas
Statmenas bisektorius
trikampis yra statmuo, nubrėžtas į trikampio kraštinės vidurį.


Trys statmenos trikampio pusiausvyros susikerta viename taške ir yra apskritimo centras.
Smailiojo trikampio statmenų bisektorių susikirtimo taškas yra trikampio viduje; buku kampu - už trikampio ribų; stačiakampėje - hipotenuzės viduryje.
Išvada
Atlikdami darbą darome tokias išvadas:
Tikslas pasiektas:ištyrinėjo trikampį ir rado nuostabius jo taškus.
Buvo išspręstos pavestos užduotys:
1). Studijavome reikiamą literatūrą;
2). Mes ištyrėme žymių trikampio taškų klasifikaciją;
3). Išmokome sukurti nuostabius trikampio taškus;
4). Apibendrinome išstuduotą medžiagą bukleto dizainui.
Pasitvirtino hipotezė, kad gebėjimas rasti reikšmingus trikampio taškus padeda spręsti konstravimo problemas.
Darbe nuosekliai nubrėžiami žymių trikampio taškų konstravimo būdai ir pateikiama istorinė informacija apie geometrines konstrukcijas.
Informacija iš šio darbo gali būti naudinga geometrijos pamokose 7 klasėje. Knygelė gali tapti geometrijos žinynu pateikta tema.
Bibliografija
Vadovėlis. L.S. Atanasjanas „Geometrijos 7-9 klMnemosyne, 2015 m.
Vikipedijahttps://ru.wikipedia.org/wiki/Geometry#/media/File:Euclid%27s_postulates.png
Scarlet Sails portalas
Pirmaujantis švietimo portalas Rusijoje http://cendomzn.ucoz.ru/index/0-15157
KETURI PAŽYMI TAŠKAI
TRIKAMPIS
Geometrija
8 klasė
Sacharova Natalija Ivanovna
Simferopolio MBOU 28 vidurinė mokykla

- Trikampio medianų susikirtimo taškas
- Trikampio bisektorių susikirtimo taškas
- Trikampio aukščių susikirtimo taškas
- Trikampio statmenų medianų susikirtimo taškas

Mediana
Mediana (BD) trikampis yra atkarpa, jungianti trikampio viršūnę su priešingos kraštinės vidurio tašku.

Medianos trikampiai susikerta vienu metu (gravitacijos centras trikampis) ir yra padalinti iš šio taško santykiu 2: 1, skaičiuojant nuo viršūnės.

BIEKTORIAUS
Bisektorius (AD) trikampis yra trikampio vidinio kampo pusiausvyros segmentas. ∟
BLOGAS = ∟CAD.

Kiekvienas taškas bisektorius neišsivysčiusio kampo yra vienodu atstumu nuo jo kraštų.
Atgal:
kiekvienas taškas, esantis kampo viduje ir vienodai nutolęs nuo kampo kraštų, yra ant jo bisektorius.

Visi bisektoriniai trikampiai susikerta viename taške - užrašo centras
į trikampį apskritimai.
Apskritimo spindulys (OM) yra statmenas, nusileidęs iš centro (TO) į trikampio kraštinę

AUKŠTIS
Aukštis (CD) trikampis yra statmena atkarpa, nubrėžta iš trikampio viršūnės į tiesę, kurioje yra priešinga kraštinė.

Aukštumos trikampiai (ar jų plėtiniai) susikerta vienas tašką.

VIDURINIS STAMELAS
Statmenas bisektorius (DF) vadinama tiese, statmena trikampio kraštinei ir dalijančia ją pusiau.

Kiekvienas taškas statmenas bisektorius(m) iki atkarpos yra vienodu atstumu nuo šios atkarpos galų.
Atgal:
kiekvienas taškas, esantis vienodu atstumu nuo atkarpos galų, yra vidurio taške statmenai jam.

Visos trikampio kraštinių statmenos pusės susikerta viename taške - aprašytojo centras
šalia trikampio ratas
.
Apskritimo apskritimo spindulys yra atstumas nuo apskritimo centro iki bet kurios trikampio viršūnės (OA).

Puslapis 177 Nr.675 (brėžinys)

Namų darbai
P. 173 § 3 apibrėžimai ir teoremos p. 177 Nr. 675 (pabaiga)
Baranova Elena
Šiame darbe nagrinėjami svarbūs trikampio taškai, jų savybės ir modeliai, tokie kaip devynių taškų apskritimas ir Eulerio tiesė. Pateikiamas istorinis Eulerio tiesės ir devynių taškų apskritimo atradimo fonas. Pasiūlyta praktinė mano projekto taikymo kryptis.
Parsisiųsti:
Peržiūra:
Norėdami naudoti pristatymų peržiūras, susikurkite „Google“ paskyrą ir prisijunkite prie jos: https://accounts.google.com
Skaidrių antraštės:
„NUOSTABIŪS TRIKAMPIO TAŠKAI“. (Matematikos taikomieji ir pagrindiniai klausimai) Elena Baranova 8 klasė, MKOU “20 vidurinė mokykla” Poz. Novoizobilny, Dukhanina Tatjana Vasiljevna, matematikos mokytoja, Savivaldybės švietimo įstaiga "20 vidurinė mokykla" Novoizobilny kaimas 2013. Savivaldybės švietimo įstaiga "Vidurinė mokykla Nr. 20"
Tikslas: ištirti trikampio žymius taškus, ištirti jų klasifikaciją ir savybes. Uždaviniai: 1. Išstudijuoti reikiamą literatūrą 2. Išstudijuoti trikampio žymiųjų taškų klasifikaciją 3.. Susipažinti su trikampio žymiųjų taškų savybėmis 4. Mokėti konstruoti trikampio žymiuosius taškus. 5. Ištirkite svarbių dalykų apimtį. Studijų objektas – matematikos skyrius – geometrija Studijų objektas – trikampis Aktualumas: praplėskite savo žinias apie trikampį, jo žymių taškų savybes. Hipotezė: trikampio ir gamtos ryšys
Statmenų bisektorių susikirtimo taškas yra vienodu atstumu nuo trikampio viršūnių ir yra apibrėžto apskritimo centras. Aplink trikampius apibrėžti apskritimai, kurių viršūnės yra trikampio kraštinių vidurio taškai, o trikampio viršūnės susikerta viename taške, kuris sutampa su statmenų bisektorių susikirtimo tašku.
Bisektorių susikirtimo taškas Trikampio pusiaukampių susikirtimo taškas yra vienodu atstumu nuo trikampio kraštinių. OM=OA=OB
Aukščių susikirtimo taškas Trikampio, kurio viršūnės yra aukščių pagrindai, pusiaukampių susikirtimo taškas sutampa su trikampio aukščių susikirtimo tašku.
Medianų susikirtimo taškas Trikampio medianos susikerta viename taške, kuris kiekvieną medianą dalija santykiu 2:1, skaičiuojant nuo viršūnės. Jei medianų susikirtimo taškas yra sujungtas su viršūnėmis, tada trikampis bus padalintas į tris vienodo ploto trikampius. Svarbi medianų susikirtimo taško savybė yra ta, kad vektorių, kurių pradžia yra medianų susikirtimo taškas, o galai yra trikampių viršūnės, suma yra lygi nuliui M1 N C B A m2 m3 M1 N C B A m2 m3 M1 N C B A m2 m3 M1 N C B A m2 m3
Torricelli taškas Pastaba: Torricelli taškas egzistuoja, jei visi trikampio kampai yra mažesni nei 120.
Devynių taškų apskritimas B1, A1, C1 – aukščių pagrindai; A2, B2, C2 – atitinkamų kraštinių vidurio taškai; A3, B3, C3 yra atkarpų AN, VN ir CH vidurio taškai.
Eulerio tiesė Medianų susikirtimo taškas, aukščių susikirtimo taškas, devynių taškų apskritimo centras yra vienoje tiesėje, kuri vadinama Eulerio tiesia matematiko, kuris nustatė šį modelį, garbei.
Šiek tiek iš nuostabių taškų atradimo istorijos 1765 m. Euleris atrado, kad trikampio kraštinių vidurio taškai ir jo aukščių pagrindai yra tame pačiame apskritime. Įspūdingiausia nuostabių trikampio taškų savybė yra ta, kad kai kurie iš jų yra sujungti vienas su kitu tam tikru santykiu. Medianų M susikirtimo taškas, aukščių H susikirtimo taškas ir apskritimo O centras yra toje pačioje tiesėje, o taškas M padalija atkarpą OH taip, kad santykis OM: OH = 1: 2 yra Šią teoremą įrodė Leonhardas Euleris 1765 m.
Geometrijos ir gamtos ryšys. Šioje padėtyje potenciali energija turi mažiausią reikšmę ir atkarpų MA+MB+MC suma bus mažiausia, o vektorių, esančių ant šių atkarpų su pradžia Torricelli taške, suma bus lygi nuliui.
Išvados Sužinojau, kad be man žinomų nuostabių aukščių, vidurių, pusiau ir statmenų sankirtos taškų, taip pat yra nuostabių trikampio taškų ir linijų. Šia tema įgytas žinias gebėsiu panaudoti savo edukacinėje veikloje, savarankiškai taikyti teoremas tam tikroms problemoms spręsti, išmoktas teoremas pritaikyti realioje situacijoje. Manau, kad mokantis matematikos naudoti nuostabius trikampio taškus ir linijas yra efektyvu. Jų žinojimas žymiai pagreitina daugelio užduočių sprendimą. Siūloma medžiaga gali būti naudojama tiek matematikos pamokose, tiek popamokinėje veikloje 5-9 klasių mokiniams.
Peržiūra:
Norėdami naudoti peržiūrą, susikurkite „Google“ paskyrą ir prisijunkite:








 kraštinių vidurio taškai Δ ABC; leisti H
1
ir H yra jų ortocentrai (65 pav.). Taškas H 1 sutampa su centru APIE apskritimas Δ ABC.Įrodykime, kad Δ
kraštinių vidurio taškai Δ ABC; leisti H
1
ir H yra jų ortocentrai (65 pav.). Taškas H 1 sutampa su centru APIE apskritimas Δ ABC.Įrodykime, kad Δ